题目内容
6.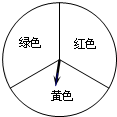 甲、乙两位同学玩转盘游戏,游戏规则:将圆盘平均分成三份,分别涂上红,黄,绿三种颜色,两位同学分别转动转盘两次(若压线,重新转).若两次指针指到的颜色
甲、乙两位同学玩转盘游戏,游戏规则:将圆盘平均分成三份,分别涂上红,黄,绿三种颜色,两位同学分别转动转盘两次(若压线,重新转).若两次指针指到的颜色相同,则甲获胜;若两次指针指到的颜色是黄绿组合则乙获胜;其余情况则视为平局.
请用画树状图或列表的方法,用概率说明游戏是否公平.
分析 先画树状图展示所有9种等可能的结果数,再找出两次指针指到的颜色相同的结果数和两次指针指到的颜色是黄绿组合的结果数,则可根据概率公式计算甲、乙获胜的概率,然后比较概率的大小即可判断游戏是否公平.
解答 解:这个游戏不公平.理由如下:
画树状图为: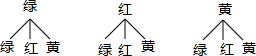
共有9种等可能的结果数,其中两次指针指到的颜色相同的结果数为3,两次指针指到的颜色是黄绿组合的结果数为2,
所以甲获胜的概率=$\frac{3}{9}$=$\frac{1}{3}$,乙获胜的概率=$\frac{2}{9}$,
因为$\frac{1}{3}$>$\frac{2}{9}$,
所以这个游戏不公平.
点评 本题考查了游戏的公平性:判断游戏公平性需要先计算每个事件的概率,然后比较概率的大小,概率相等就公平,否则就不公平.也考查了列表法与树状图法.

练习册系列答案
相关题目
1.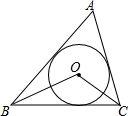 如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=( )
如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=( )
 如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=( )
如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=( )| A. | 100° | B. | 75° | C. | 115° | D. | 105° |
11. 如图,点A、B、P为⊙O上的点,若∠APB=15°,则∠AOB=( )
如图,点A、B、P为⊙O上的点,若∠APB=15°,则∠AOB=( )
 如图,点A、B、P为⊙O上的点,若∠APB=15°,则∠AOB=( )
如图,点A、B、P为⊙O上的点,若∠APB=15°,则∠AOB=( )| A. | 15° | B. | 20° | C. | 30° | D. | 45° |
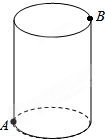 如图,圆柱的高为5cm,底面周长为12cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是$\sqrt{61}$厘米.
如图,圆柱的高为5cm,底面周长为12cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是$\sqrt{61}$厘米.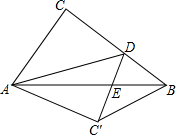 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为$\frac{3}{2}$或$\frac{3}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为$\frac{3}{2}$或$\frac{3}{4}$.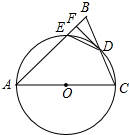 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为点F,连接DE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为点F,连接DE.