题目内容
18. 如图.在?ABCD中,AB=5,AD=8,DE平分∠ADC,求BE的长.
如图.在?ABCD中,AB=5,AD=8,DE平分∠ADC,求BE的长.
分析 先根据角平分线和平行四边形的性质求出CD=CE,再由BE=BC-CE求解.
解答 解:∵在?ABCD中,AB=5,AD=8,
∴BC=8,CD=5,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
又?ABCD中,AD∥BC,
∴∠ADE=∠DEC,
∴∠DEC=∠CDE,
∴CD=CE=5,
∴BE=BC-CE=8-5=3.
点评 本题主要考查平行四边形的性质,角平分线性质的利用是解题的关键,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.

练习册系列答案
相关题目
6.下面说法正确的是( )
| A. | 一个三角形经过适当的旋转得到的图形和原图形可组成平行四边形 | |
| B. | 一个三角形经过适当的平移,前后图形可组成平行四边形 | |
| C. | 因为正方形也可以看作菱形,故菱形经过适当的旋转可得到正方形 | |
| D. | 夹在两平行直线之间的线段相等 |
3.下列变形属于分解因式的是( )
| A. | 2x2-4x+1=2x(x-2)+1 | B. | m(a+b+c)=ma+mb+mc | ||
| C. | x2-y2=(x+y)(x-y) | D. | (m-n)(b+a)=(b+a)(m-n) |
7.已知a<b,则下列式子正确的是( )
| A. | a-1>b-1 | B. | -3a<-3b | C. | -2a>-2b | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
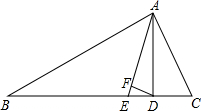 如图,在△ABC中,∠B=25°,∠C=65°,AD⊥BC于D,AE平分∠BAC交BC于E,DF⊥AE.
如图,在△ABC中,∠B=25°,∠C=65°,AD⊥BC于D,AE平分∠BAC交BC于E,DF⊥AE.