题目内容
4.计算:$\frac{a+1}{(a-1)^{2}}$•$\frac{{a}^{2}-3a+2}{{a}^{2}-a-2}$-$\frac{{a}^{2}}{{a}^{2}-1}$÷$\frac{a}{a+1}$=-1.分析 原式先计算乘除运算,再计算加减运算即可得到结果.
解答 解:原式=$\frac{(a+1)}{(a-1)^{2}}$•$\frac{(a-1)(a-2)}{(a-2)(a+1)}$-$\frac{{a}^{2}}{(a+1)(a-1)}$•$\frac{a+1}{a}$=$\frac{1}{a-1}$-$\frac{a}{a-1}$=$\frac{1-a}{a-1}$=-$\frac{a-1}{a-1}$=-1,
故答案为:-1
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.记A=$\sum_{k=1}^{2013}$$\sqrt{1+\frac{1}{{k}^{2}}+\frac{1}{(k+1)^{2}}}$,再记[A]表示不超过A的最大整数,则[A]( )
| A. | 2010 | B. | 2011 | C. | 2012 | D. | 2013 |
13. 如图,菱形ABCD中,AC=16,BD=12,则菱形的周长是( )
如图,菱形ABCD中,AC=16,BD=12,则菱形的周长是( )
 如图,菱形ABCD中,AC=16,BD=12,则菱形的周长是( )
如图,菱形ABCD中,AC=16,BD=12,则菱形的周长是( )| A. | 20 | B. | 24 | C. | 28 | D. | 40 |
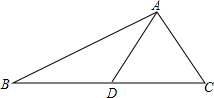 如图所示,在△ABC中,AD是BC边上的中线,且AD=$\frac{1}{2}$BC.
如图所示,在△ABC中,AD是BC边上的中线,且AD=$\frac{1}{2}$BC.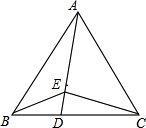 如图,等边△ABC中,D在BC边上,E为AD上一点,若CD=2BD,∠BEC=120°,BE=1,则CE的长度为$\sqrt{2}$.
如图,等边△ABC中,D在BC边上,E为AD上一点,若CD=2BD,∠BEC=120°,BE=1,则CE的长度为$\sqrt{2}$.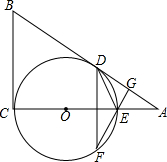 如图,已知AB和BC分别与圆O相切于点D、C,AC经过圆心O交圆于点E,AC=2AD且BD=2.
如图,已知AB和BC分别与圆O相切于点D、C,AC经过圆心O交圆于点E,AC=2AD且BD=2.