题目内容
4. 如图,E,F分别是正方形ABCD边DC,AD上一点.
如图,E,F分别是正方形ABCD边DC,AD上一点.(1)若EF=BE,∠ABF=30°,AF=3,求CE的长;
(2)若BF是∠ABE的平分线,求证:BE-AF=CE.
分析 (1)根据30°角的直角三角形的性质得出BF=2AF=6,进而根据勾股定理得出AB=3$\sqrt{3}$,连接EF,设CE=x,则DE=3$\sqrt{3}$-x,DF=3$\sqrt{3}$-3,根据EF=BE,得出(3$\sqrt{3}$-3)2+(3$\sqrt{3}$-x)2=(3$\sqrt{3}$)2+x2,解得x的值即可;
(2)延长EC到G,使CG=AF,连接BG,通过△BAF≌△BCG得出∠G=∠AFB,∠ABF=∠CBG,进而根据角平分线的性质得出∠ABF=∠FBE=∠CBG,从而得出∠EBG=∠FBC,然后根据平行线的性质得出∠AFB=∠FBC,进而得出∠EBG=∠G,根据等角对等边即可证得BE=EG=EC+CG=EC+AF,得出结论.
解答  解:(1)在RT△ABF中,∵∠ABF=30°,AF=3,
解:(1)在RT△ABF中,∵∠ABF=30°,AF=3,
∴BF=2AF=6,
∴AB=$\sqrt{B{F}^{2}-A{F}^{2}}$=3$\sqrt{3}$,
连接EF,设CE=x,则DE=3$\sqrt{3}$-x,DF=3$\sqrt{3}$-3,
∵EF=BE,
∴(3$\sqrt{3}$-3)2+(3$\sqrt{3}$-x)2=(3$\sqrt{3}$)2+x2,
解得x=2$\sqrt{3}$-3,
∴CE=2$\sqrt{3}$-3;
(2)延长EC到G,使CG=AF,连接BG,
在△BAF和△BCG中,
$\left\{\begin{array}{l}{BA=BC}\\{∠A=∠BCG=90°}\\{AF=CG}\end{array}\right.$,
∴△BAF≌△BCG(SAS),
∴∠G=∠AFB,∠ABF=∠CBG,
∵BF是∠ABE的平分线,
∴∠ABF=∠FBE=∠CBG,
∴∠EBG=∠FBC,
∵AD∥BC,
∴∠AFB=∠FBC,
∴∠EBG=∠G,
∴BE=EG=EC+CG=EC+AF,
∴BE-AF=CE.
点评 本题考查了正方形的性质,30°角的直角三角形的性质,勾股定理的应用,角平分线的性质,全等三角形的判定和性质,等腰三角形的判定等,作出辅助线构建全等三角形是解题的关键.

| x | 0 | 0.5 | 1 | 1.1 | 1.2 | 1.3 |
| x2+px+q | -15 | -8.75 | -2 | -0.59 | 0.84 | 2.29 |
| A. | 0.5<x<1 | B. | 1<x<1.1 | C. | 1.1<x<1.2 | D. | 1.2<x<1.3 |
 为解的二元一次方程组是( )
为解的二元一次方程组是( ) B.
B.  C.
C.  D.
D. 
 的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )
的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )
 C. 2 D. 2
C. 2 D. 2
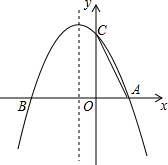 如图,已知抛物线y=ax2+bx+c与x轴交于A(m,0),B(n,0),点A位于点B的右侧,且m,n是一元二次方程x2+2x-3=0的两个根,与y轴交于C(0,3).在抛物线上的对称轴上是否存在点P,使得△PAC为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
如图,已知抛物线y=ax2+bx+c与x轴交于A(m,0),B(n,0),点A位于点B的右侧,且m,n是一元二次方程x2+2x-3=0的两个根,与y轴交于C(0,3).在抛物线上的对称轴上是否存在点P,使得△PAC为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.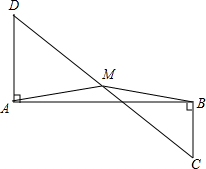 已知,如图,DA⊥AB,CB⊥AB,M是DC的中点,求证:MA=MB.
已知,如图,DA⊥AB,CB⊥AB,M是DC的中点,求证:MA=MB.