题目内容
9.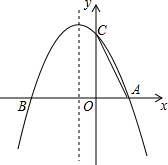 如图,已知抛物线y=ax2+bx+c与x轴交于A(m,0),B(n,0),点A位于点B的右侧,且m,n是一元二次方程x2+2x-3=0的两个根,与y轴交于C(0,3).在抛物线上的对称轴上是否存在点P,使得△PAC为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
如图,已知抛物线y=ax2+bx+c与x轴交于A(m,0),B(n,0),点A位于点B的右侧,且m,n是一元二次方程x2+2x-3=0的两个根,与y轴交于C(0,3).在抛物线上的对称轴上是否存在点P,使得△PAC为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
分析 解方程求得A和B的坐标,求得对称轴,当A是直角顶点时,求得过A于AC垂直的直线与抛物线的对称轴的交点,然后判断是否是等腰三角形;同理当C是直角顶点时利用相同的方法判断;当AC是等腰三角形的底边时,求得AC的中垂线与对称轴的交点,然后判断是否是直角三角形即可.
解答 解:解方程x2+2x-3=0得x1=-3,x2=1,
则A的坐标是(1,0),B的坐标是(-3,0).
抛物线的对称轴是x=-1.
设AC的解析式是y=kx+b,则$\left\{\begin{array}{l}{k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-3}\\{b=3}\end{array}\right.$,
则直线AC的解析式是y=-3x+3.
当A是直角顶点时,过A且垂直于AC的直线解析式设是y=$\frac{1}{3}$x+c,
把A代入得:$\frac{1}{3}$+c=0,
解得:c=-$\frac{1}{3}$,
则解析式是y=$\frac{1}{3}$x-$\frac{1}{3}$.
令x=-1,则y=-$\frac{1}{3}$-$\frac{1}{3}$=-$\frac{2}{3}$,
则交点是(-1,-$\frac{2}{3}$).到A的距离是$\sqrt{(-1-1)^{2}+(-\frac{2}{3})^{2}}$=$\frac{2\sqrt{10}}{3}$,AC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
则三角形不是等腰三角形;
同理,当C时直角时,过C于AC垂直的直线的解析式是y=$\frac{1}{3}$x+3,与对称轴x=-1的交点是(-1,$\frac{8}{3}$).到C的距离是$\sqrt{(-1-1)^{2}+(\frac{8}{3})^{2}}$=$\frac{10}{3}$≠AC,则不是等腰直角三角形;
当P是直角,即AC是斜边时,AC的中点是($\frac{1}{2}$,$\frac{3}{2}$),过这点且与AC垂直的直线的解析式是y=$\frac{1}{3}$x+$\frac{8}{6}$.
当x=-1时,y=-$\frac{1}{3}$+$\frac{8}{6}$=1.
则与对称轴的交点是(-1,1).则到A的距离是$\sqrt{(-1-1)^{2}+{1}^{2}}$=$\sqrt{5}$.
∵($\sqrt{5}$)2+($\sqrt{5}$)2=($\sqrt{10}$)2,
∴P的坐标是(-1,1).
点评 本题考查了二次函数与x轴的交点以及等腰直角三角形的判定,正确进行讨论是关键.

| A. | (22016,0) | B. | (-21008,0) | C. | (21008,0) | D. | (0,-21008) |
 x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为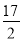 m.
m.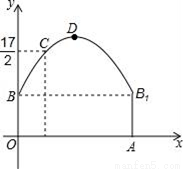
 如图,E,F分别是正方形ABCD边DC,AD上一点.
如图,E,F分别是正方形ABCD边DC,AD上一点.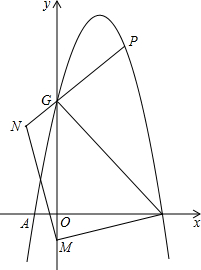 抛物线y=-x2+3x+4与x轴交于A,B两点,与y轴交于点C,如图,点M为y轴负半轴上一动点,点N在y轴左侧,MN⊥MB,MN=MB,连接NC交抛物线于点P,求点P的坐标.
抛物线y=-x2+3x+4与x轴交于A,B两点,与y轴交于点C,如图,点M为y轴负半轴上一动点,点N在y轴左侧,MN⊥MB,MN=MB,连接NC交抛物线于点P,求点P的坐标.
 如图,在平面直角坐标系中,等腰Rt△ABC中,∠ABC=90°,点E是点C关于点B的对称点,A(0,3),B(-1,0),则点E的坐标是(2,-1).
如图,在平面直角坐标系中,等腰Rt△ABC中,∠ABC=90°,点E是点C关于点B的对称点,A(0,3),B(-1,0),则点E的坐标是(2,-1).