题目内容
16.已知抛物线y=(k-1)x2+2kx+k-1,若抛物线与x轴交于A、B两点,与y轴交于C点,且△ABC的面积为4,试求k的值.分析 令x=0,可得y=k-1,令y=0,抛物线与x轴交于A、B两点,交点为(x1,0)(x2,0),可得|x1-x2|=$\sqrt{\frac{4{k}^{2}-4(k-1)^{2}}{(k-1)^{2}}}$,利用△ABC的面积为4,建立方程,即可求k的值.
解答 解:令x=0,可得y=k-1,令y=0,
抛物线与x轴交于A、B两点,交点为(x1,0)(x2,0),
AB=|x1-x2|=$\sqrt{\frac{4{k}^{2}-4(k-1)^{2}}{(k-1)^{2}}}$,
OC=|k-1|
S△ABC=$\frac{1}{2}$AB•OC=$\sqrt{\frac{4{k}^{2}-4(k-1)^{2}}{(k-1)^{2}}}$•|k-1|=4,
4k-4(k-2k+1)=64,
解得:k=$\frac{17}{2}$.
点评 此题考查抛物线与x轴的交点坐标,三角形的面积,利用两点之间的距离表示出AB之间的距离是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.平面直角坐标系中,已知点P0(1,0),将点P0绕原点O按逆时针方向旋转30°得到P1,延长OP1到P2,使OP2=2OP1;再将P2绕点O按逆时针方向旋转30°得P3,然后延长OP3到P4,使OP4=2OP3;…;如此下去.则点P2016的坐标为( )
| A. | (22016,0) | B. | (-21008,0) | C. | (21008,0) | D. | (0,-21008) |
 ,
,  ,则
,则 ( )
( ) (x>0)的图象相交于点A,B,设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形面积和周长分别为_____、_____.
(x>0)的图象相交于点A,B,设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形面积和周长分别为_____、_____.
 如图,E,F分别是正方形ABCD边DC,AD上一点.
如图,E,F分别是正方形ABCD边DC,AD上一点.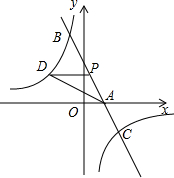 如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5),C($\frac{5}{2}$,d)两点,点M是y轴上一动点,点P(m,n)是一次函数y=kx+b的图象上的动点.
如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5),C($\frac{5}{2}$,d)两点,点M是y轴上一动点,点P(m,n)是一次函数y=kx+b的图象上的动点.