题目内容
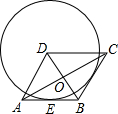 如图,在菱形ABCD中,AB=2
如图,在菱形ABCD中,AB=2| 3 |
(1)求AC的长;
(2)求证:⊙D与边BC也相切.
考点:切线的判定与性质,菱形的性质
专题:
分析:(1)由菱形的性质得∴∠BAO=30°,∠AOB=90°,AC=2AO,再求得AO的值即可得AC;
(2)连接DE,过点D作DF⊥BC,垂足为点F,由菱形的性质可得BD平分∠ABC,根据角平分线的性质可得DF=DE,得出⊙D与边BC也相切.
(2)连接DE,过点D作DF⊥BC,垂足为点F,由菱形的性质可得BD平分∠ABC,根据角平分线的性质可得DF=DE,得出⊙D与边BC也相切.
解答:(1)解:∵四边形ABCD是菱形,∠BAD=60°
∴∠BAO=30°,∠AOB=90°,AC=2AO
∴AO=AB•cos∠BAO=2
×cos30°=3
∴AC=6.
(2)证明:连接DE,过点D作DF⊥BC,垂足为点F
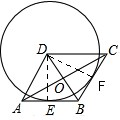
∵四边形ABCD是菱形,∴BD平分∠ABC
∵⊙D与边AB相切于点E,∴DE⊥AB
∵DF⊥BC
∴DF=DE
∴⊙D与边BC也相切.
∴∠BAO=30°,∠AOB=90°,AC=2AO
∴AO=AB•cos∠BAO=2
| 3 |
∴AC=6.
(2)证明:连接DE,过点D作DF⊥BC,垂足为点F

∵四边形ABCD是菱形,∴BD平分∠ABC
∵⊙D与边AB相切于点E,∴DE⊥AB
∵DF⊥BC
∴DF=DE
∴⊙D与边BC也相切.
点评:本题主要考查了菱形的性质、解直角三角形、圆的切线的判定及性质.知识点较多,综合性强,关键是对这些知识的熟练掌握.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
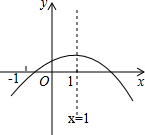 已知二次函数图象y=ax2+bx+c(a≠0)的图象如图,有下列4个结论.
已知二次函数图象y=ax2+bx+c(a≠0)的图象如图,有下列4个结论.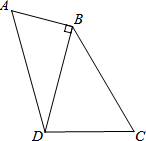 如图,在四边形ABCD中,AB=2,∠A=∠C=60°,DB⊥AB于点B,∠DBC=45°,求BC的长.
如图,在四边形ABCD中,AB=2,∠A=∠C=60°,DB⊥AB于点B,∠DBC=45°,求BC的长. 已知:如图,在平面直角坐标系xOy中,点A(2
已知:如图,在平面直角坐标系xOy中,点A(2