题目内容
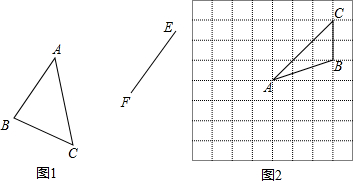
8.为发展电信事业,方便用户,电信公司对移动电话采用不同的收费方式,所使用的便民卡和如意卡在本市范围内每月(30天)的通话时间x(分钟)与通话费y(元)的关系如图所示,图中y1表示便民卡,y2 表示如意卡:
(1)图中A点的坐标有什么含义;
(2)两种卡每分钟的通话费用是多少?
(3)分别求出通话费y1、y2与通话时间x之间的函数关系式.当一个月通话时间超过100分钟时选择哪种卡更合算?
分析 (1)由图象可得点A的坐标表示便民卡每月的月租费是29元;
(2)分别利用待定系数法求一次函数解析式和待定系数法求正比例函数解析式求解,然后把x=2代入解答即可;
(3)把通话时间代入函数关系式求出两种卡的费用,即可得解.
解答 解:(1)图中A点的坐标表示便民卡每月的月租费是29元;
(2)便民卡:设y1=kx+b,
则$\left\{\begin{array}{l}{b=29}\\{30k+b=35}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=0.2}\\{b=29}\end{array}\right.$,
所以,y1=0.2x+29;
如意卡:设y2=mx,
则30m=15,
解得m=0.5,
所以,y2=0.5x;
把x=2代入y1=0.2x+29=29.4;
把x=2代入y2=0.5x=1;
答:两种卡每分钟的通话费用是便民卡是29.4元,如意卡是1元;
(3)由(2)可得:y1=0.2x+29;y2=0.5x;
把x=100代入y1=0.2x+29=49;
把x=100代入y2=0.5x=50;
所以可得当一个月通话时间超过100分钟时选择便民卡合算.
点评 本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,读懂题目信息并准确识图是解题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
18.下列图形中,既是中心对称图形又有且只有两条对称轴对称图形是( )
| A. | 正三角形 | B. | 正方形 | C. | 圆 | D. | 菱形 |
 如图,直线y=kx+b与直线y=2x交于点C(1,m),直线y=kx+b与坐标轴分别交于点A,B.
如图,直线y=kx+b与直线y=2x交于点C(1,m),直线y=kx+b与坐标轴分别交于点A,B. 如图,等腰三角形ABC的周长为18,CD为腰AB边上的中线,△ACD与△BCD的周长差为3(AC>BC),则底边BC的长度是( )
如图,等腰三角形ABC的周长为18,CD为腰AB边上的中线,△ACD与△BCD的周长差为3(AC>BC),则底边BC的长度是( )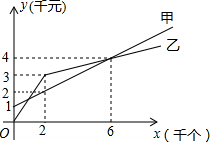 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲乙两厂的印刷费用y(千元)与证书数量x(千个)的函数关系图象分别如图中甲、乙所示.
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲乙两厂的印刷费用y(千元)与证书数量x(千个)的函数关系图象分别如图中甲、乙所示. 如图,已知线段m,n,求作线段AB,使AB=2m+n.
如图,已知线段m,n,求作线段AB,使AB=2m+n.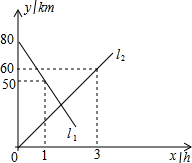 如图,A、B两地相距80km,甲、乙两人骑车分别从A、B两地同时相向而行,他们都保持匀速行驶,l1,l2分别表示甲、乙两人离B地的距离y/km与骑车时间x/h的函数关系.
如图,A、B两地相距80km,甲、乙两人骑车分别从A、B两地同时相向而行,他们都保持匀速行驶,l1,l2分别表示甲、乙两人离B地的距离y/km与骑车时间x/h的函数关系.