题目内容
20.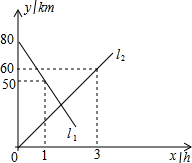 如图,A、B两地相距80km,甲、乙两人骑车分别从A、B两地同时相向而行,他们都保持匀速行驶,l1,l2分别表示甲、乙两人离B地的距离y/km与骑车时间x/h的函数关系.
如图,A、B两地相距80km,甲、乙两人骑车分别从A、B两地同时相向而行,他们都保持匀速行驶,l1,l2分别表示甲、乙两人离B地的距离y/km与骑车时间x/h的函数关系.经过多长时间两人相遇?相遇时甲离A地多远?
分析 利用待定系数法求出一次函数和正比例函数解析式解答即可.
解答 解:设l2=kx,则60=k×3,解得:k=20,故l2=20x;
设l1=ax+b,将(0,80),(1,50),则
$\left\{\begin{array}{l}{80=b}\\{50=a+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-30}\\{b=80}\end{array}\right.$,
故l1=-30x+80;
当两人相遇时,可得:20x=-30x+80,
解得:x=1.6,
把x=1.6代入l2=20x=32,
答:经过1.6小时两人相遇,相遇时甲离A地32km.
点评 此题主要考查了一次函数的应用,根据题意求出函数解析式是解题关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
10.已知关于x的一元二次方程(a+c)x2+2bx+a-c=0,其中a、b、c分别为△ABC三边的长.下列关于这个方程的解和△ABC形状判断的结论错误的是( )
| A. | 如果x=-1是方程的根,则△ABC是等腰三角形 | |
| B. | 如果方程有两个相等的实数根,则△ABC是直角三角形 | |
| C. | 如果△ABC是等边三角形,方程的解是x=0或x=-1 | |
| D. | 如果方程无实数解,则△ABC是锐角三角形 |
5. 某仓库调拨一批物资(调进与调出物资的速度均保持不变),该仓库库存物资m(吨)与时间t(小时)之间的函数关系如图所示,则这批物资从开始调进到全部调出所需要的时间是( )
某仓库调拨一批物资(调进与调出物资的速度均保持不变),该仓库库存物资m(吨)与时间t(小时)之间的函数关系如图所示,则这批物资从开始调进到全部调出所需要的时间是( )
 某仓库调拨一批物资(调进与调出物资的速度均保持不变),该仓库库存物资m(吨)与时间t(小时)之间的函数关系如图所示,则这批物资从开始调进到全部调出所需要的时间是( )
某仓库调拨一批物资(调进与调出物资的速度均保持不变),该仓库库存物资m(吨)与时间t(小时)之间的函数关系如图所示,则这批物资从开始调进到全部调出所需要的时间是( )| A. | 8.4小时 | B. | 8.6小时 | C. | 8.8小时 | D. | 9小时 |
9.在0,3,-1,$\frac{1}{2}$中最小的数是( )
| A. | 0 | B. | 3 | C. | -1 | D. | $\frac{1}{2}$ |
 如图,直线l1∥l2,直线AB交直线l1,l2于D,B两点,AC⊥AB交直线l1于C.若∠1=40°40′,则∠2=130°40′.
如图,直线l1∥l2,直线AB交直线l1,l2于D,B两点,AC⊥AB交直线l1于C.若∠1=40°40′,则∠2=130°40′.
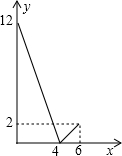 甲、乙两人分别从A、B两地同时出发,相向而行,相遇后,甲立即返回,乙的方向不变,且甲先到A地,两人相距的路程y(千米)与行驶时间x(小时)之间的函数关系的图象如图所示,则甲的速度为:1.75千米/小时.
甲、乙两人分别从A、B两地同时出发,相向而行,相遇后,甲立即返回,乙的方向不变,且甲先到A地,两人相距的路程y(千米)与行驶时间x(小时)之间的函数关系的图象如图所示,则甲的速度为:1.75千米/小时.