Question

14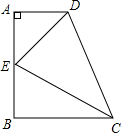．（1）如图，AD∥BC，∠A=90°，∠DCB的角平分线CE与∠ADC的角平分线DE恰好相交于AB的点E，试猜想CD、AD、BC之间的数量关系，并说明理由
（2）在（1）中，若∠A≠90°，其他条件保持不变，你的猜想还成立吗？请画出草图，并说明理由．

Answer 1

分析 （1）过点E作EF⊥DC，由角平分线的性质可知：AE=EF，然后证明Rt△ADE≌Rt△FDE，可知；AD=DF，同理可知BC=FC；
（2）在DC上取DF=AD，连接EF．首先证明△ADE≌△FDE，得到∠A=∠DFE，然后证明△BEC≌△FEC，从而可证得AD+BC=DC．

解答 解：（1）CD=AD+BC．
理由：如图所示，过点E作EF⊥DC．

∵AD∥BC，∠A=90°，
∴∠B=90°．
∵EA⊥AD，EF⊥DC，DE平分∠ADC，
∴AE=EF．
在Rt△ADE和Rt△FDE中$\left\{\begin{array}{l}{AE=EF}\\{DE=DE}\end{array}\right.$，
∴Rt△ADE≌Rt△FDE．
∴AD=FC．
同理：FC=BC．
∴AD+BC=DC．
（2）成立．
如图所示，在DC上取DF=AD，连接EF．

证明：∵ED平分∠ADF，
∴∠ADE=∠FDE，
在△ADE和△FDE中，$\left\{\begin{array}{l}{AD=DF}\\{∠ADE=∠FDE}\\{DE=DE}\end{array}\right.$，
∴△ADE≌△FDE．
∴∠A=∠DFE．
∵AD∥BC，
∴∠DAB+∠ABC=180°．
又∵∠DFE+∠EFC=180°，
∴∠B=∠EFC．
在△BEC和△FEC中，$\left\{\begin{array}{l}{∠B=∠EFC}\\{∠FCE=∠BCE}\\{EC=EC}\end{array}\right.$，
∴△BEC≌△FEC．
∴FC=BC．
∴AD+BC=DC．

点评 本题考查了全等三角形的性质和判定，平行线的性质，角平分线定义等知识点的应用，关键是能正确作辅助线．