题目内容
19.在Rt△ABC中,∠C=90°,∠A=60°,斜边上的高是$\sqrt{3}$,则a=2$\sqrt{3}$,b=2,c=4.分析 利用直角三角形的性质求得∠B,根据含30°直角三角形的性质、锐角三角函数的意义求得各边即可.
解答 解:如图,
∵∠C=90°,∠A=60°,CD=$\sqrt{3}$,
∴∠B=30°,
∴a=2CD=2$\sqrt{3}$,
b=$\frac{a}{tan∠A}$=$\frac{2\sqrt{3}}{\sqrt{3}}$=2,
c=4.
故答案为:2$\sqrt{3}$,2,4.
点评 此题考查解直角三角形,掌握锐角三角函数的意义以及含30°直角三角形的性质是解决问题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
8.下列logo标志中,是中心对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.计算$\sqrt{2}$×$\sqrt{3}$的结果是( )
| A. | $\sqrt{5}$ | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{6}$ |
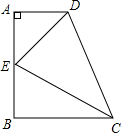 (1)如图,AD∥BC,∠A=90°,∠DCB的角平分线CE与∠ADC的角平分线DE恰好相交于AB的点E,试猜想CD、AD、BC之间的数量关系,并说明理由
(1)如图,AD∥BC,∠A=90°,∠DCB的角平分线CE与∠ADC的角平分线DE恰好相交于AB的点E,试猜想CD、AD、BC之间的数量关系,并说明理由