题目内容
2.(1)解不等式组:$\left\{\begin{array}{l}{3x-2≤x+6①}\\{x+5>4x+2②}\end{array}\right.$(2)因式分解:a-2a2+a3
(3)解分式方程:$\frac{x}{x-2}-\frac{1}{x}=1$.
分析 (1)求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可;
(2)先提公因式,再根据完全平方公式分解即可;
(3)方程两边都乘以x(x-2)得出整式方程,求出方程的解,再进行检验即可.
解答 解:(1)∵由①得:2x≤8,
x≤4,
由②得:-3x>2-5,
x<1,
∴原不等式组的解集是x<1;
(2)a-2a2+a3
=a(1-2a+a2)
=a(1-a)2;
(3)$\frac{x}{x-2}-\frac{1}{x}=1$
解:方程两边都乘以x(x-2)得:x2-(x-2)=x(x-2),
解得:x2-x+2=x2-2x,
2x-x=-2,
x=-2,
经检验:x=-2是原方程的根,
所以原方程的解为x=-2.
点评 本题考查了解一元一次不等式组,解分式方程,分解因式的应用,能综合运用知识点进行计算是解此题的关键.

练习册系列答案
相关题目
17.下列因式分解正确的是( )
| A. | a(x+y)=ax+ay | B. | 10t2-5t=5t(2t-1) | ||
| C. | y2-4y+3=(y-2)2-1 | D. | x2-16+3x=(x+4)(x-4)+3x |
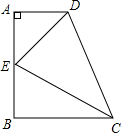 (1)如图,AD∥BC,∠A=90°,∠DCB的角平分线CE与∠ADC的角平分线DE恰好相交于AB的点E,试猜想CD、AD、BC之间的数量关系,并说明理由
(1)如图,AD∥BC,∠A=90°,∠DCB的角平分线CE与∠ADC的角平分线DE恰好相交于AB的点E,试猜想CD、AD、BC之间的数量关系,并说明理由