题目内容
4. 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OBC=20°.
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OBC=20°.
分析 根据圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半得:∠BOC=2∠BAC,在等腰三角形OBC中可求出∠OCB.
解答 解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=70°,
∴∠OBC=20°,
故答案为:20°.
点评 此题考查了圆周角定理,熟练掌握直径所对的圆周角是直角是解题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
15.已知x=2+$\sqrt{3}$,y=$\sqrt{3}$-2,则x与y的关系是( )
| A. | x=y | B. | x=-y | C. | xy=1 | D. | xy=-1 |
9.计算$\sqrt{2}$×$\sqrt{3}$的结果是( )
| A. | $\sqrt{5}$ | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{6}$ |
16. 如图,点A、B、C都在圆O上,如果∠AOB+∠ACB=84°,那么∠ACB的大小是( )
如图,点A、B、C都在圆O上,如果∠AOB+∠ACB=84°,那么∠ACB的大小是( )
 如图,点A、B、C都在圆O上,如果∠AOB+∠ACB=84°,那么∠ACB的大小是( )
如图,点A、B、C都在圆O上,如果∠AOB+∠ACB=84°,那么∠ACB的大小是( )| A. | 28° | B. | 30° | C. | 32° | D. | 42° |
14.计算(-5)×(-6)÷3的结果是( )
| A. | 10 | B. | -10 | C. | $-\frac{5}{2}$ | D. | $\frac{5}{2}$ |
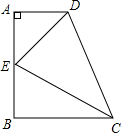 (1)如图,AD∥BC,∠A=90°,∠DCB的角平分线CE与∠ADC的角平分线DE恰好相交于AB的点E,试猜想CD、AD、BC之间的数量关系,并说明理由
(1)如图,AD∥BC,∠A=90°,∠DCB的角平分线CE与∠ADC的角平分线DE恰好相交于AB的点E,试猜想CD、AD、BC之间的数量关系,并说明理由