题目内容
14.若a+b+c=0,a2+b2+c2=1,a4+b4+c4=$\frac{1}{2}$.分析 要想求a4+b4+c4的值,只需要根据a+b+c=0,a2+b2+c2=1,两边平方,然后整理即可建立与a4+b4+c4的关系,从而可以解答本题.
解答 解:∵a+b+c=0,
∴(a+b+c)2=0,
即a2+b2+c2+2ab+2bc+2ac=0,
∵a2+b2+c2=1,
∴a2+b2+c2+2ab+2bc+2ac=1+2ab+2bc+2ac=0,
即$ab+bc+ac=-\frac{1}{2}$,
∴$(ab+bc+ac)^{2}=\frac{1}{4}$,
即a2b2+b2c2+a2c2+2ab2c+2abc2+2a2bc=$\frac{1}{4}$,
∴a2b2+b2c2+a2c2+2abc(b+c+a)=a2b2+b2c2+a2c2+2×0=a2b2+b2c2+a2c2=$\frac{1}{4}$,
∵(a2+b2+c2)2=12,
即a4+b4+c4+2a2b2+2b2c2+2a2c2=1,
∴a4+b4+c4=1-2a2b2-2b2c2-2a2c2=1-2(a2b2+b2c2+a2c2)=1-$2×\frac{1}{4}=1-\frac{1}{2}=\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查完全平方公式,解题的关键是灵活变化,对题目中的式子整理建立与所求式子的关系,需要注意的是变形过程中一定要仔细认真.

练习册系列答案
相关题目
20.若关于x的分式方程$\frac{2x-m}{n-2x}$=$\frac{p}{q}$有解,则必须满足条件( )
| A. | m≠n | B. | m≠-n | C. | np≠-mq | D. | p≠-q,m≠n |
9.△ABC中,AC=4,BC=3,AB=5,tanA的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
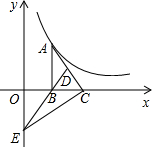 如图,Rt△ABC的直角边BC在x轴正半轴上,点D为AC上一点,且AD=3DC,BD的反向延长线交y轴负半轴于E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BEC=6,则k=36.
如图,Rt△ABC的直角边BC在x轴正半轴上,点D为AC上一点,且AD=3DC,BD的反向延长线交y轴负半轴于E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BEC=6,则k=36. 如图,PA、PB是⊙O的切线,A、B分别为切点,PO交圆于点C,若∠APB=60°,PC=6,则AC的长为2$\sqrt{3}$.
如图,PA、PB是⊙O的切线,A、B分别为切点,PO交圆于点C,若∠APB=60°,PC=6,则AC的长为2$\sqrt{3}$.