题目内容
7.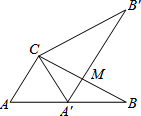 如图,△ABC中,∠ACB=90°,∠B=30°,BC=6,三角板绕C逆时针旋转,当点A的对应点A′落在AB边上时即停止转动,则BM的长为3.
如图,△ABC中,∠ACB=90°,∠B=30°,BC=6,三角板绕C逆时针旋转,当点A的对应点A′落在AB边上时即停止转动,则BM的长为3.
分析 首先可求得∠A=60°,然后由旋转的性质可知∠A=∠A′=60°,AC=A′C,可知△ACA′为等边三角形,接下来由等腰三角形三线合一的性质可知:CM=BM.
解答 解:∵∠ACB=90°,∠B=30°,
∴∠A=60°.
由旋转的性质可知:AC=AC′,∠A=∠A′=60°
∴△ABA′为等边三角形.
∴∠ACA′=60°.
∴∠A′CB=30°.
∴∠A′CB=∠B.
∴A′C=A′B.
∵∠A′CB=30°,∠A′=60°,
∴∠CMA′=90°.
∵∠CMA′=90°,A′C=A′B,
∴CM=BM.
∴BM=$\frac{1}{2}BC\frac{1}{2}×6=3$.
故答案为:3.
点评 本题考查了旋转的性质以及等边三角形的判定,旋转前后对应角相等,证得∠CMA′=90°,A′C=A′B是解题的关键.

练习册系列答案
相关题目
15.已知正比例函数y=(2m+3)x的图象上两点A(x1,y1)和 A(x2,y2),当x1<x2时y1>y2,则m的取值范围是( )
| A. | $m<-\frac{3}{2}$ | B. | $m>-\frac{3}{2}$ | C. | $0<m<\frac{3}{2}$ | D. | m<0 |
2.在三边分别为下列长度的三角形中,不是直角三角形的是( )
| A. | 5,12,13 | B. | 4,5,9 | C. | 2,3,$\sqrt{5}$ | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
 如图,AB∥CD,E、F分别是BC、AD的中点,且AB=a,CD=b,则EF的长为$\frac{1}{2}$(b-a).
如图,AB∥CD,E、F分别是BC、AD的中点,且AB=a,CD=b,则EF的长为$\frac{1}{2}$(b-a).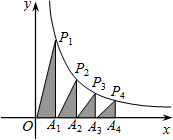 如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3…=A2014A2015=1,过点A1、A2、A3、…、A2015分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、…P2015,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、…A2014P2015A2015,并设其面积分别为S1、S2、S3、…S2015,则S2015的值为$\frac{1}{2015}$.
如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3…=A2014A2015=1,过点A1、A2、A3、…、A2015分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、…P2015,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、…A2014P2015A2015,并设其面积分别为S1、S2、S3、…S2015,则S2015的值为$\frac{1}{2015}$.