题目内容
12.已知一次函数y=kx+b(k、b为常数且k≠0)的图象经过点A(3,2),点B(1,0).求一次函数y=kx+b的解析式.分析 利用待定系数法把A(3,2),B(1,0)代入一次函数y=kx+b,可得到一个关于k、b的方程组,再解方程组即可得到k、b的值,然后即可得到一次函数的解析式.
解答 解:∵一次函数y=kx+b的图象经过两点A(3,2),B(1,0),
∴$\left\{\begin{array}{l}{3k+b=2}\\{k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
∴一次函数解析式为:y=x-1
点评 此题主要考查了待定系数法求一次函数解析式,关键是掌握待定系数法求一次函数解析式一般步骤是:
(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;
(2)将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;
(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
相关题目
2.在三边分别为下列长度的三角形中,不是直角三角形的是( )
| A. | 5,12,13 | B. | 4,5,9 | C. | 2,3,$\sqrt{5}$ | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
3.下列命题中是假命题的是( )
| A. | 同旁内角互补,两直线平行 | |
| B. | 直线a⊥b,则a 与b的夹角为直角 | |
| C. | 如果两个角互补,那么这两个角一个是锐角,一个是钝角 | |
| D. | 若a∥b,a⊥c,那么b⊥c |
1.在△ABC中,已知cosB=$\frac{3}{5}$,sinC=$\frac{2}{3}$,AC=2,那么边AB等于( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{20}{9}$ | D. | $\frac{12}{5}$ |
2.一个直角三角形的一条直角边长为5,斜边长为13,则另一条直角边的长是( )
| A. | 12 | B. | 10 | C. | $\sqrt{194}$ | D. | 以上答案都不是 |
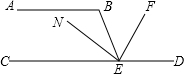 如图,AB∥CD,点E在CD上,EN平分∠BEC,EF⊥EN.若∠B=110°,则∠DEF=55°.
如图,AB∥CD,点E在CD上,EN平分∠BEC,EF⊥EN.若∠B=110°,则∠DEF=55°.