题目内容
2.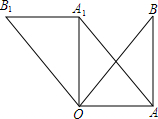 如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°
如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°得到△OA1B1.
(1)线段A1B1的长是6,∠AOA1的度数是90°;
(2)连结AA1,求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积.
分析 (1)根据旋转的性质即可直接求解;
(2)根据旋转的性质以及平行线的判定定理证明B1A1∥OA且A1B1=OA即可证明四边形OAA1B1是平行四边形;
(3)利用平行四边形的面积公式求解.
解答 解:(1)A1B1=AB=6,∠AOA1=90°.
故答案是:6,90°;
(2)∵A1B1=AB=6,OA1-OA=6,∠OA1B1=∠OAB=90°,∠AOA1=90°,
∴∠OA1B1=∠AOA1,A1B1=OA,
∴B1A1∥OA,
∴四边形OAA1B1是平行四边形;
(3)S=OA•A1O=6×6=36.
即四边形OAA1B1的面积是36.
点评 本题考查了旋转的性质以及平行四边形的判定和面积公式,证明B1A1∥OA是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.若二次函数y=ax2+c的图象开口向下,则( )
| A. | a>0 | B. | a<0 | C. | c>0 | D. | c<0 |
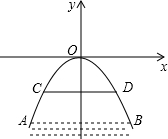 如图是以拱桥最高点为坐标原点,建立直角坐标系的抛物线拱桥.已知水在AB位置时,水面宽4$\sqrt{6}$米,水面距离桥顶12米.当水位上升达到警戒线CD时水面宽4$\sqrt{3}$米,若洪水到来时,水位以每小时0.6米速度上升.求水过警戒线后几小时淹到拱桥顶?
如图是以拱桥最高点为坐标原点,建立直角坐标系的抛物线拱桥.已知水在AB位置时,水面宽4$\sqrt{6}$米,水面距离桥顶12米.当水位上升达到警戒线CD时水面宽4$\sqrt{3}$米,若洪水到来时,水位以每小时0.6米速度上升.求水过警戒线后几小时淹到拱桥顶? 如图的组合图案可以看作是由一个正方形和正方形内通过一个“基本图案”半圆进行图形的“运动”变换而组成的,这个半圆的变换方式是旋转.
如图的组合图案可以看作是由一个正方形和正方形内通过一个“基本图案”半圆进行图形的“运动”变换而组成的,这个半圆的变换方式是旋转.
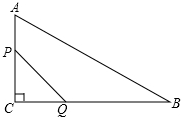 如图,△ABC中,∠C=90°,AC=12,BC=6,点P从A开始沿AC边向C点以1个单位每秒的速度移动.同时Q点从C沿边CB以2个单位每秒的速度向点B移动.设移动时间为t,请解答下列问题:
如图,△ABC中,∠C=90°,AC=12,BC=6,点P从A开始沿AC边向C点以1个单位每秒的速度移动.同时Q点从C沿边CB以2个单位每秒的速度向点B移动.设移动时间为t,请解答下列问题: