题目内容
12.在实数范围内把x2-2x-1分解因式为(x-1+$\sqrt{2}$)(x-1-$\sqrt{2}$).分析 先把前面两项配成完全平方式,然后根据平分差公式进行因式分解即可.
解答 解:x2-2x-1,
=x2-2x+1-2,
=(x-1)2-2,
=(x-1+$\sqrt{2}$)(x-1-$\sqrt{2}$).
故答案为:(x-1+$\sqrt{2}$)(x-1-$\sqrt{2}$).
点评 本题考查了利用公式进行因式分解的方法:把整式先配成完全平分式或平分差的形式,然后利用公式法进行因式分解.

练习册系列答案
相关题目
7.$\sqrt{7}$x2-x=0的根是( )
| A. | x=$\frac{\sqrt{7}}{7}$ | B. | x1=0,x2=$\frac{\sqrt{7}}{7}$ | C. | x1=0,x2=$\sqrt{7}$ | D. | x=$\sqrt{7}$ |
1.最小的细胞是支原体,有一种支原体的细胞的直径是0.21954微米,将这个数精确到千分位是( )
| A. | 0.219 | B. | 0.21 | C. | 0.220 | D. | 0.2195 |
2.下列计算正确的是( )
| A. | 2a-a=1 | B. | 2x2y-3xy2=-xy2 | C. | 4a2+5a2=9a4 | D. | 3ax-2xa=ax |
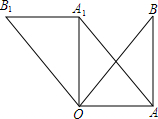 如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°
如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°