题目内容
在△ABC中,AD是角平分线,若∠B=50°,∠C=70°,则∠ADC= .
考点:三角形内角和定理
专题:
分析:先根据三角形内角和定理求出∠BAC的度数,再由角平分线的性质求出∠DAC的度数,根据三角形内角和定理即可得出结论.
解答: 解:∵△ABC中∠B=50°,∠C=70°,
解:∵△ABC中∠B=50°,∠C=70°,
∴∠BAC=180°-∠B-∠C=180°-50°-70°=60°,
∵AD是角平分线,
∴∠DAC=
∠BAC=
×60°=30°.
在△ACD中,
∵∠DAC=30°,∠C=70°,
∴∠ADC=180°-∠DAC-∠C=180°-30°-70°=80°.
故答案为:80°.
 解:∵△ABC中∠B=50°,∠C=70°,
解:∵△ABC中∠B=50°,∠C=70°,∴∠BAC=180°-∠B-∠C=180°-50°-70°=60°,
∵AD是角平分线,
∴∠DAC=
| 1 |
| 2 |
| 1 |
| 2 |
在△ACD中,
∵∠DAC=30°,∠C=70°,
∴∠ADC=180°-∠DAC-∠C=180°-30°-70°=80°.
故答案为:80°.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
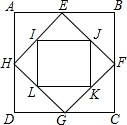 如图,ABCD为60cm×80cm的矩形窗户,内嵌有菱形窗格EFGH和矩形IJKL.矩形窗格IJKL的四个顶点恰好位于菱形窗格EFGH各边的中点.求矩形窗格IJKL的各边长和面积.
如图,ABCD为60cm×80cm的矩形窗户,内嵌有菱形窗格EFGH和矩形IJKL.矩形窗格IJKL的四个顶点恰好位于菱形窗格EFGH各边的中点.求矩形窗格IJKL的各边长和面积. 如图,在等腰三角形ABC中,AB=AC,AD是底边BC上的高,AB=5cm,BC=6cm,求AD的长.
如图,在等腰三角形ABC中,AB=AC,AD是底边BC上的高,AB=5cm,BC=6cm,求AD的长.