题目内容
20.已知:a2+b2=3,ab=1,求下列各式的值:(1)$\frac{b}{a}$+$\frac{a}{b}$;
(2)$\frac{{b}^{2}}{{a}^{2}}$+$\frac{{a}^{2}}{{b}^{2}}$;
(3)$\frac{b}{a}$-$\frac{a}{b}$.
分析 根据分式的运算即可求出答案.
解答 解:(1)∵a2+b2=3,ab=1
原式=$\frac{{b}^{2}+{a}^{2}}{ab}$=$\frac{3}{1}$
=3
(2)∵$\frac{b}{a}$+$\frac{a}{b}$=3
原式=($\frac{b}{a}+\frac{a}{b}$)2-2
=9-2
=7
(3)∵$\frac{{b}^{2}}{{a}^{2}}$+$\frac{{a}^{2}}{{b}^{2}}$=7
($\frac{b}{a}$-$\frac{a}{b}$)2=$\frac{{b}^{2}}{{a}^{2}}$+$\frac{{a}^{2}}{{b}^{2}}$-2
=7-2
=5
∴$\frac{b}{a}$-$\frac{a}{b}$=$±\sqrt{5}$
点评 本题考查完全平方公式,解题的关键是熟练运用完全平方公式,本题属于基础题型.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
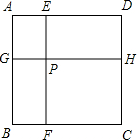 如图,边长为a的正方形ABCD被两条与边平行的线段EF、GH分割成四个小矩形,EF与GH交于点P,连接AF、AH.
如图,边长为a的正方形ABCD被两条与边平行的线段EF、GH分割成四个小矩形,EF与GH交于点P,连接AF、AH.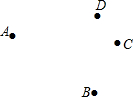 已知平面上A,B,C,D四个点,按下列要求画出图形:
已知平面上A,B,C,D四个点,按下列要求画出图形: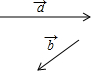 如图,已知向量$\overrightarrow{a}$、$\overrightarrow{b}$,求作$\overrightarrow{AB}$=3$\overrightarrow{a}$+2$\overrightarrow{b}$.
如图,已知向量$\overrightarrow{a}$、$\overrightarrow{b}$,求作$\overrightarrow{AB}$=3$\overrightarrow{a}$+2$\overrightarrow{b}$.