题目内容
9. 如图是5×5方格子(每个小正方格的边长为1个单位长度),图中阴影部分是正方形,则此正方形的边长为( )
如图是5×5方格子(每个小正方格的边长为1个单位长度),图中阴影部分是正方形,则此正方形的边长为( )| A. | 3 | B. | $\sqrt{7}$ | C. | $\sqrt{13}$ | D. | 5 |
分析 根据每一个小方格都是边长为1个单位长度的正方形,再根据勾股定理,列出算式,即可得出答案.
解答 解:根据题意得:
阴影正方形的边长是:$\sqrt{{2}^{2}+{3}^{2}}=\sqrt{13}$;
故选C
点评 此题考查了算术平方根,用到的知识点是算术平方根的求法和勾股定理,关键是根据勾股定理列出算式.

练习册系列答案
相关题目
4. 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )
 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2015次后,数轴上数2015所对应的点是( )| A. | 点C | B. | 点D | C. | 点A | D. | 点B |
14.对于任意不相等的两个实数a、b,定义运算※如下:a※b=$\frac{\sqrt{a+b}}{a-b}$;例如3※2=$\frac{\sqrt{3+2}}{3-2}$=$\sqrt{5}$.那么5※7等于( )
| A. | $-\sqrt{3}$ | B. | -4 | C. | $-2\sqrt{3}$ | D. | -3 |
19.在学习“用直尺和圆规作一个角等于已知角”时,教科书介绍如下:
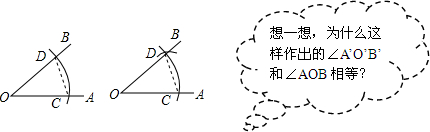
作法:
(1)如图所示,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧相交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB
对于“想一想”中的问题,下列回答正确的是( )

作法:
(1)如图所示,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧相交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB
对于“想一想”中的问题,下列回答正确的是( )
| A. | 根据“边边边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| B. | 根据“边角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| C. | 根据“角边角”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| D. | 根据“角角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB |
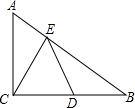 如图,在△ABC中,AC=BC=$\sqrt{5}$,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值是$\frac{5}{2}$.
如图,在△ABC中,AC=BC=$\sqrt{5}$,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值是$\frac{5}{2}$. 如图所示,是由5个大小相同的立方体搭起来的一个几何体,则从左面看到的它的形状图是( )
如图所示,是由5个大小相同的立方体搭起来的一个几何体,则从左面看到的它的形状图是( )



 如图是一数值转换机,若输入的x为-4,则输出的结果为10.
如图是一数值转换机,若输入的x为-4,则输出的结果为10.