题目内容
4.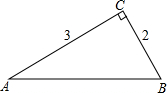 如图,在Rt△ABC中,∠C=Rt∠,AC=3,BC=2.求sinA,cosA,tanA.
如图,在Rt△ABC中,∠C=Rt∠,AC=3,BC=2.求sinA,cosA,tanA.
分析 根据勾股定理,可得AB的长,根据在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
解答 解:在Rt△ABC中,由勾股定理,得
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$.
sinA=$\frac{BC}{AB}$=$\frac{2}{\sqrt{13}}$=$\frac{2\sqrt{13}}{13}$,
cosA=$\frac{AC}{AB}$=$\frac{3}{\sqrt{13}}$=$\frac{3\sqrt{13}}{13}$,
tanA=$\frac{BC}{AC}$=$\frac{2}{3}$.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
14.今年我省某一天的天气预报中,张家口市的最低气温为-6℃,石家庄市的最低气温为2℃,那么,这一天张家口市的气温比石家庄市低( )
| A. | 8℃ | B. | -8℃ | C. | 6℃ | D. | 2℃ |
12.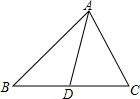 如图,△ACD∽△BCA,则下列各式中一定成立的是( )
如图,△ACD∽△BCA,则下列各式中一定成立的是( )
 如图,△ACD∽△BCA,则下列各式中一定成立的是( )
如图,△ACD∽△BCA,则下列各式中一定成立的是( )| A. | $\frac{AC}{CD}$=$\frac{AB}{BC}$ | B. | $\frac{CD}{AD}$=$\frac{BC}{AC}$ | C. | CD2=AD•DB | D. | AC2=CD•BC |
9.下列说法正确的是( )
| A. | -|-2|=-(-2) | B. | (-1)2n=1(n是正整数) | ||
| C. | -(-a-b)=a-b | D. | 2x3y-3x2y-1是三次三项式 |
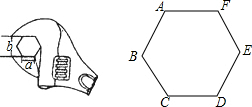 如图,要打开一个边长a=12mm的六角形螺帽(下图的正六边形ABCDEF是六角形螺帽的放大图),扳手张开的开口b至少要多少??
如图,要打开一个边长a=12mm的六角形螺帽(下图的正六边形ABCDEF是六角形螺帽的放大图),扳手张开的开口b至少要多少??