题目内容
 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=5,EC=3,则DE的长为( )
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=5,EC=3,则DE的长为( )| A、2 | B、3 | C、4 | D、5 |
考点:勾股定理,等腰三角形的判定与性质,直角三角形斜边上的中线
专题:计算题
分析:由AD与BC平行,且DE垂直于BC,得到DE垂直于AD,在直角三角形AED中,利用斜边上的中线等于斜边的一半,得到DG=GF,作GH⊥DE,利用三线合一得到GH为角平分线,再由∠ACD=2∠ACB,等量代换得到∠DGF=∠ACD,等角对等边得到DG=DC=5,在直角三角形CDE中,利用勾股定理求出DE的长即可.
解答:
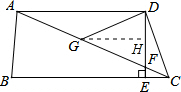 解:∵AD∥BC,DE⊥BC,
解:∵AD∥BC,DE⊥BC,
∴∠ADF=∠DEC=90°,
∵点G是AF的中点,
∴DG=GF,
作GH⊥DE于H,则GH∥BC,
∵∠HGF=∠ACB,
∵∠DGF=2∠HGF,∠ACD=2∠ACB,
∴∠DGF=∠ACD,
∴CD=DG=5,
又∵∠DEC=90°,EC=3,
∴DE=
=4.
故选C
 解:∵AD∥BC,DE⊥BC,
解:∵AD∥BC,DE⊥BC,∴∠ADF=∠DEC=90°,
∵点G是AF的中点,
∴DG=GF,
作GH⊥DE于H,则GH∥BC,
∵∠HGF=∠ACB,
∵∠DGF=2∠HGF,∠ACD=2∠ACB,
∴∠DGF=∠ACD,
∴CD=DG=5,
又∵∠DEC=90°,EC=3,
∴DE=
| CD2-EC2 |
故选C
点评:此题考查了勾股定理,等腰三角形的性质,平行线的性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
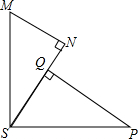 如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,添加下列条件能使△MNS≌△SQP的是( )
如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,添加下列条件能使△MNS≌△SQP的是( )| A、∠A=∠QSP |
| B、∠MSN=∠P |
| C、MS=SP |
| D、MN=QN |
一直三角形的两边长分别为3和4,则第三边长为( )
| A、5 | ||
B、5或
| ||
C、
| ||
| D、以上都不对 |
 如图,△ABC中,∠A=90°,试说明AB+AC>BC.
如图,△ABC中,∠A=90°,试说明AB+AC>BC.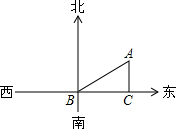 一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东59°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,求这艘船航行的速度.(精确到1海里/时)
一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东59°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,求这艘船航行的速度.(精确到1海里/时) 如图所示,已知△ABC的三个内角度数之比是∠A:∠B:∠C=1:2:3,若设BC=a,AC=b,AB=c
如图所示,已知△ABC的三个内角度数之比是∠A:∠B:∠C=1:2:3,若设BC=a,AC=b,AB=c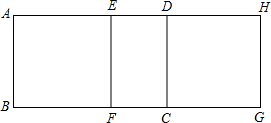 如图,长方形ABCD,AB=5cm,AD=8cm.若将该长方形沿AD方向平移一段距离,得到长方形EFGH,试问:
如图,长方形ABCD,AB=5cm,AD=8cm.若将该长方形沿AD方向平移一段距离,得到长方形EFGH,试问: