题目内容
无论k为何值,抛物线y=-x2+(k-2)x+3(k+1)的顶点总在某条曲线上,求该定曲线的解析式.
考点:二次函数的性质
专题:
分析:把二次函数的解析式化成顶点式,根据顶点式即可求得顶点曲线的解析式.
解答:
解:由题意可知:y=-x2+(k-2)x+3(k+1)=-(x-
)+
,
∴顶点的纵坐标为y=
,
∴该定曲线的解析式为y=
(k+4)2.
| k-2 |
| 2 |
| (k+4)2 |
| 4 |
∴顶点的纵坐标为y=
| (k+4)2 |
| 4 |
∴该定曲线的解析式为y=
| 1 |
| 4 |
点评:本题考查了二次函数的性质,把解析式化成顶点式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列语句是命题的是( )
| A、作线段AB的中点 |
| B、作线段AB的垂直平分线 |
| C、等角的补角相等吗? |
| D、对顶角不相等 |
图中,∠1和∠2是同位角的是( )
A、 |
B、 |
C、 |
D、 |
估算
的值( )
| 13 |
| A、在1与2之间 |
| B、2.5与3之间 |
| C、3与3.5之间 |
| D、3.5与4之间 |
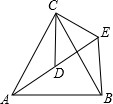 如图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
如图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.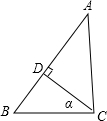 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设∠BCD=α,若sinα=
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设∠BCD=α,若sinα=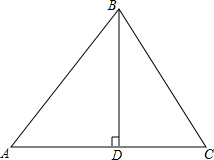 如图,△ABC中,BD⊥AC,AB=15cm,AC=24cm,∠A=60°.求BC的长.
如图,△ABC中,BD⊥AC,AB=15cm,AC=24cm,∠A=60°.求BC的长. 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=5,EC=3,则DE的长为( )
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=5,EC=3,则DE的长为( ) 如图,在数轴上点A表示数a,点B表示数b,AB表示点A和点B之间的距离,且a,b满足|a+2|+(b+3a)2=0
如图,在数轴上点A表示数a,点B表示数b,AB表示点A和点B之间的距离,且a,b满足|a+2|+(b+3a)2=0