题目内容
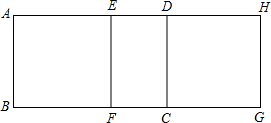 如图,长方形ABCD,AB=5cm,AD=8cm.若将该长方形沿AD方向平移一段距离,得到长方形EFGH,试问:
如图,长方形ABCD,AB=5cm,AD=8cm.若将该长方形沿AD方向平移一段距离,得到长方形EFGH,试问:(1)长方形ABFE与长方形DCGH的面积是否相等?
(2)将长方形ABCD平移多长距离,能使两长方形的重叠部分FCDE的面积是35cm2?
考点:平移的性质
专题:
分析:(1)根据平移的性质直接得出即可.
(2)设线段AE=x,则ED=AD-AE=8-x,因为BC=8,所以矩形EFCD的面积为ED•AB=35cm2,就可以列出方程,解方程即可;
(2)设线段AE=x,则ED=AD-AE=8-x,因为BC=8,所以矩形EFCD的面积为ED•AB=35cm2,就可以列出方程,解方程即可;
解答:
解:(1)面积相等:
∵矩形EFGH是由矩形ABCD平移得到的,
∴矩形ABCD的面积和矩形EFGH的面积相等,
∴长方形ABFE与长方形DCGH的面积相等;
(2)设AE=x,根据题意列出方程:5(8-x)=35,
解得x=1,
∵A的对应点为E,
∴平移距离为AE的长,
故向右平移1cm,能使两长方形的重叠部分FCDE的面积是35cm2.
∵矩形EFGH是由矩形ABCD平移得到的,
∴矩形ABCD的面积和矩形EFGH的面积相等,
∴长方形ABFE与长方形DCGH的面积相等;
(2)设AE=x,根据题意列出方程:5(8-x)=35,
解得x=1,
∵A的对应点为E,
∴平移距离为AE的长,
故向右平移1cm,能使两长方形的重叠部分FCDE的面积是35cm2.
点评:本题综合考查了平移的性质和一元一次方程的应用,关键是扣住矩形EFCD的面积为35cm2,运用方程思想求解.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
图中,∠1和∠2是同位角的是( )
A、 |
B、 |
C、 |
D、 |
计算4a3÷(-2a2)的结果是( )
| A、-a | B、-2a | C、a | D、2a |
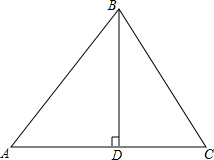 如图,△ABC中,BD⊥AC,AB=15cm,AC=24cm,∠A=60°.求BC的长.
如图,△ABC中,BD⊥AC,AB=15cm,AC=24cm,∠A=60°.求BC的长. 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=5,EC=3,则DE的长为( )
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=5,EC=3,则DE的长为( ) 如图,B,C,F,E在同一直线上,AB∥DE,AC∥DF,BF=CE,
如图,B,C,F,E在同一直线上,AB∥DE,AC∥DF,BF=CE, 如图所示,已知直线AB和x轴交于点B,和y轴交于点A
如图所示,已知直线AB和x轴交于点B,和y轴交于点A 如图,在数轴上点A表示数a,点B表示数b,AB表示点A和点B之间的距离,且a,b满足|a+2|+(b+3a)2=0
如图,在数轴上点A表示数a,点B表示数b,AB表示点A和点B之间的距离,且a,b满足|a+2|+(b+3a)2=0