题目内容
4.一次函数y=(m-2)x+m2-1的图象经过点A(0,3)(1)求m的值,并写出函数解析式;
(2)若(1)中的函数图象与x轴交于点B,直线y=(m+2)x+m2-1也经过A(0,3)且与x轴交于点C,求线段BC的长.
分析 (1)根据题意知一次函数y=(m-2)x+m2-1的图象经过点(0,3),所以将其代入一次函数解析式,然后解关于m的方程即可.
(2)据题意知一次函数y=(m+2)x+m2-1的图象也经过点(0,3),所以将其代入一次函数解析式,然后解关于m的方程即可求得解析式,进而求得B、C的坐标,从而求得线段BC的长.
解答 解:(1)∵一次函数y=(m-2)x+m2-1的图象经过(0,3)点,
∴3=0+m2-1,即m2=4,
解得,m=±2.
∵m-2≠0,
∴m=-2
∴函数解析式为:y=-4x+3.
(2)∵y=(m+2)x+m2-1也经过A(0,3),
∴3=0+m2-1,即m2=4,
解得,m=±2.
∵m+2≠0,
∴m=2
∴函数解析式为:y=4x+3.
∴B($\frac{3}{4}$,0),C(-$\frac{3}{4}$,0),
∴BC=$\frac{3}{4}$-(-$\frac{3}{4}$)=$\frac{3}{2}$.
点评 本题考查了待定系数法求一次函数的解析式以及直线和x轴的交点,根据待定系数法求得解析式是本题的关键.

练习册系列答案
相关题目
19.多项式(x2+y2)(x2+y2-8)+16分解因式正确的是( )
| A. | (x2+y2-4)2 | B. | (x-y)4 | C. | (x2-y2-4)2 | D. | (x2+y2+4)2 |
9. 关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )
关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )
 关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )
关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )| A. | -6 | B. | -12 | C. | 6 | D. | 12 |
 如图,反比例函数y=$\frac{k}{x}$图象与一次函数y=-x-1图象的一个交点为A(-2,a).
如图,反比例函数y=$\frac{k}{x}$图象与一次函数y=-x-1图象的一个交点为A(-2,a).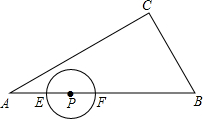 如图,在Rt△ABC中,∠C=90°,BC=3,∠A=30°,点P在AB上,AP=2.点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也运动到点B时停止.在点E、F运动过程中,以EF为直径作圆.设点E运动的时间为t秒.
如图,在Rt△ABC中,∠C=90°,BC=3,∠A=30°,点P在AB上,AP=2.点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也运动到点B时停止.在点E、F运动过程中,以EF为直径作圆.设点E运动的时间为t秒.