题目内容
5.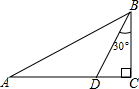 如图所示,在△ABC中,∠C=90°,AB=4$\sqrt{3}$.点D在边AC上,且AD=BD,∠DBC=30°.求:
如图所示,在△ABC中,∠C=90°,AB=4$\sqrt{3}$.点D在边AC上,且AD=BD,∠DBC=30°.求:(1)CD及AD的长度;
(2)∠BAC及∠DBA的度数.
分析 (1)由含30°角的直角三角形的性质得出CD=$\frac{1}{2}$BD,∠BDC=60°,由等腰三角形的性质和三角形的外角性质得出∠BAC=∠DBA=30°,由含30°角的直角三角形的性质得出BC=$\frac{1}{2}$AB=2$\sqrt{3}$,设CD=x,则AD=BD=2x,由勾股定理得出方程,解方程即可;
(2)由(1)得出∠BAC=∠DBA=30°.
解答 解:(1)∵∠DBC=30°,∠C=90°,
∴CD=$\frac{1}{2}$BD,∠BDC=60°,
∵AD=BD,
∴∠BAC=∠DBA,
∵∠BAC+∠DBA=∠BDC=60°,
∴∠BAC=∠DBA=30°,
∴BC=$\frac{1}{2}$AB=2$\sqrt{3}$,
设CD=x,则AD=BD=2x,
由勾股定理得:BC2+CD2=BD2,
即(2$\sqrt{3}$)2+x2=(2x)2,
解得:x=2,
∴CD=2,AD=BD=2CD=4;
(2)由(1)得:∠BAC=∠DBA=30°.
点评 本题考查了勾股定理、含30°角的直角三角形的性质、等腰三角形的性质、三角形的外角性质;熟练掌握勾股定理和等腰三角形的性质,由勾股定理得出方程是解决(1)的关键.

练习册系列答案
相关题目
10. 甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
 甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )| A. | 从一个装有2个白球和1个红球的袋子中任取两球,取到两个白球的概率 | |
| B. | 任意写一个正整数,它能被2整除的概率 | |
| C. | 抛一枚硬币,连续两次出现正面的概率 | |
| D. | 掷一枚正六面体的骰子,出现1点的概率 |
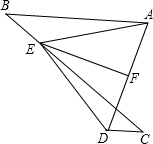 如图,已知AB∥CD,点E在BC上且BE=CD,AB=CE,EF平分∠AED.
如图,已知AB∥CD,点E在BC上且BE=CD,AB=CE,EF平分∠AED.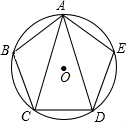 如图,正五边形ABCD内接于⊙O,连接对角线AC,AD,则下列结论:①BC∥AD;②∠BAE=3∠CAD;③△BAC≌△EAD;④AC=2CD.其中判断正确的是①②③.(填序号)
如图,正五边形ABCD内接于⊙O,连接对角线AC,AD,则下列结论:①BC∥AD;②∠BAE=3∠CAD;③△BAC≌△EAD;④AC=2CD.其中判断正确的是①②③.(填序号)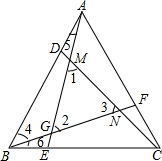 如图,△ABC为等边角形,点D,E,F分别为AB,BC,CA上的一点,且AD=BE=CF,AE,BF,CD分别相交于点G,N,M,试判断△MNG的形状并证明.
如图,△ABC为等边角形,点D,E,F分别为AB,BC,CA上的一点,且AD=BE=CF,AE,BF,CD分别相交于点G,N,M,试判断△MNG的形状并证明.