题目内容
4.平面直角坐标系中,O为坐标原点,点A的坐标为($\sqrt{3}$,1),将OA绕原点按逆时针方向旋转90°得OB,则点B的坐标为( )| A. | (1,$\sqrt{3}$) | B. | (-1,$\sqrt{3}$) | C. | (0,2) | D. | (2,0) |
分析 在平面直角坐标系中,画出图形,通过“双垂线”法构造全等三角形,利用全等三角形性质求出对应线段长度,进而求出点B的坐标.
解答 解:如图,过A做AC⊥x轴,BE⊥x轴,
∵∠AOB=90°,
∴∠BOE+∠AOC=90°,
∵∠A+∠AOC=90°,
∴∠A=∠BOE,
在△OCA和△BEO中,
$\left\{\begin{array}{l}{∠A=∠BOE}\\{∠E=∠C}\\{OA=OB}\end{array}\right.$,
△OCA≌△BEO中,
∴OE=AC=1,BE=OC=$\sqrt{3}$,
∴点B坐标为(-1,$\sqrt{3}$).
故选:B.
点评 题目考查平面直角坐标系中坐标图形的变化--旋转,通过点的旋转及全等三角形的构造,考察学生观察能力,是不错的题目.

练习册系列答案
相关题目
10. 甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
 甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )| A. | 从一个装有2个白球和1个红球的袋子中任取两球,取到两个白球的概率 | |
| B. | 任意写一个正整数,它能被2整除的概率 | |
| C. | 抛一枚硬币,连续两次出现正面的概率 | |
| D. | 掷一枚正六面体的骰子,出现1点的概率 |
16.下列说法正确的是( )
| A. | +a是正数 | B. | -a是负数 | ||
| C. | a与-a互为相反数 | D. | a与-a一定有一个是负数 |
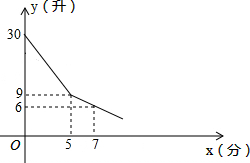 某校为学生装一台电开水器,课间操学生到开水器打水.假定每人水杯接水0.7升,他们先同时打开多个水笼头,后来因故障,关闭了故障水笼头,假设前后两人接水间隔时间忽略不计,且不发生泼洒,开水器的余水量y(升)与接水时间x(分)的函数图象如图,请结合图象回答下列问题.
某校为学生装一台电开水器,课间操学生到开水器打水.假定每人水杯接水0.7升,他们先同时打开多个水笼头,后来因故障,关闭了故障水笼头,假设前后两人接水间隔时间忽略不计,且不发生泼洒,开水器的余水量y(升)与接水时间x(分)的函数图象如图,请结合图象回答下列问题.