题目内容
一元二次方程2x(kx-4)-x2+6=0有实根,k的最大整数是 .
考点:根的判别式
专题:
分析:首先把方程整理为(2k-1)x2-8x+6=0有实根,再根据判别式的意义得到2k-1≠0且△=(-8)2-4×(2k-1)×6≥0,再解不等式得k≤2,然后找出此范围内的最大整数即可.
解答:解:原方程整理为(2k-1)x2-8x+6=0,
∵(2k-1)x2-8x+6=0有实根,
∴2k-1≠0且△=(-8)2-4×(2k-1)×6≥0,
∴k≠
,k≤2,
∴k的最大整数是2.
故答案为:2.
∵(2k-1)x2-8x+6=0有实根,
∴2k-1≠0且△=(-8)2-4×(2k-1)×6≥0,
∴k≠
| 1 |
| 2 |
∴k的最大整数是2.
故答案为:2.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列方程中,是一元一次方程的是( )
| A、x2-4x=3 | ||
| B、x+2y=1 | ||
| C、x-1=0 | ||
D、x-1=
|
 如图,把一张长方形纸沿对角线AC折叠后,顶点B落在B′处,已知∠ACB′=28°,那么,∠DCB′=( )
如图,把一张长方形纸沿对角线AC折叠后,顶点B落在B′处,已知∠ACB′=28°,那么,∠DCB′=( )| A、28° | B、31° |
| C、32° | D、34° |
 如图,已知正六边形ABCDEF和正方形AGHF,则∠ABG的度数为( )
如图,已知正六边形ABCDEF和正方形AGHF,则∠ABG的度数为( )| A、75° | B、70° |
| C、65° | D、60° |
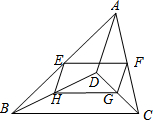 如图,D是△ABC内一点,BD⊥CD,AD=12,BD=8,CD=6,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
如图,D是△ABC内一点,BD⊥CD,AD=12,BD=8,CD=6,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( ) 如图,△ABC与△ADE都是等腰直角三角形,∠ACB与∠E都是直角,点C在AD边上,BC=
如图,△ABC与△ADE都是等腰直角三角形,∠ACB与∠E都是直角,点C在AD边上,BC= 下列是由几块小立方块搭成的几何体的主视图与左视图,这个几何体最多可能有
下列是由几块小立方块搭成的几何体的主视图与左视图,这个几何体最多可能有 小李和小陆从A地出发,骑自行车沿同一条路行驶到B地.小陆因为有事,在A地停留0.5小时后出发,1小时后他们相遇,两人约定,谁先到B地就在原地等待.他们离出发地的距离S(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图所示.
小李和小陆从A地出发,骑自行车沿同一条路行驶到B地.小陆因为有事,在A地停留0.5小时后出发,1小时后他们相遇,两人约定,谁先到B地就在原地等待.他们离出发地的距离S(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图所示.