题目内容
1．不透明袋子中装有5个红球，3个绿球，这些球只有颜色差别，若从袋子中随机摸出1个球，摸出绿球的概率是$\frac{3}{8}$．分析 根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．
解答 解：袋子中球的总数为：5+3=8，
取到绿球的概率为：$\frac{3}{8}$．
故答案为：$\frac{3}{8}$．
点评 此题主要考查了概率的求法，如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=$\frac{m}{n}$．
练习册系列答案
相关题目
11．
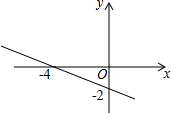一次函数y=kx+b的图象如图所示，则不等式kx+b＜0的解集是（ ）
一次函数y=kx+b的图象如图所示，则不等式kx+b＜0的解集是（ ）| A． | x＞-2 | B． | x＜-2 | C． | x＞-4 | D． | x＜-4 |
12．我市为创建“国家级森林城市”，政府将对江边一处废弃地进行绿化，要求种植甲、乙两种不同的树苗6000棵，政府以280000元将工程承包给某承包商，根据调查及相关资料表明：移栽一棵树苗的费用为8元，甲、乙两种树苗购买价和成活率如表：
政府与承包商的合同要求，栽种树苗的成活率必须不低于93%．当成活率不低于93%时，没成活的树苗政府负责出资补栽，否则，承包商出资补栽，若成活率达到94%以上（含94%），政府还另给9000元的奖励，请根据以上的信息解答下列问题：
（1）承包商要使得种植这批树苗的成活率不低于93%，甲种树苗最多栽种多少棵？
（2）已知承包商在没有补栽的情况下树苗成活率在93%以上，除开成本（购置树苗和栽种这批树苗的费用）共获得64000元，问该承包商栽种甲、乙两种树苗各多少棵？
| 品种 | 购买价 | 成活率 |
| 甲 | 20 | 90% |
| 乙 | 32 | 95% |
（1）承包商要使得种植这批树苗的成活率不低于93%，甲种树苗最多栽种多少棵？
（2）已知承包商在没有补栽的情况下树苗成活率在93%以上，除开成本（购置树苗和栽种这批树苗的费用）共获得64000元，问该承包商栽种甲、乙两种树苗各多少棵？
9．在-4，-2，0，1，3，4这六个数中，小于2的数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
10．
如图，在?ABCD中，CE⊥AB，点E为垂足，如果∠D=55°，则∠BCE=（ ）
如图，在?ABCD中，CE⊥AB，点E为垂足，如果∠D=55°，则∠BCE=（ ）| A． | 55° | B． | 35° | C． | 25° | D． | 30° |
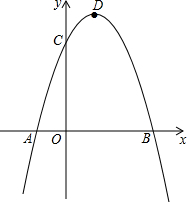已知二次函数y=ax2+bx-3a经过点A（-1，0）、C（0，3），与x轴交于另一点B，抛物线的顶点为D．