题目内容
6.在△ABC中,∠ABC=90°,D是AB边上的一点,且AD=CD,P是直线AC上任意一点,过点P作PE⊥AD于点E,PF⊥CD于点F.(1)如图1,当点P在线段AC上,猜想:线段PE、PF与BC的数量关系,并证明你的猜想;
(2)当点P在AC的延长线上时,其它条件不变,请你在图2中补全图形,并标记相应的字母,并根据补全的图形猜想PE、PF与BC又有怎样的数量关系?直接写出结论,不用证明.
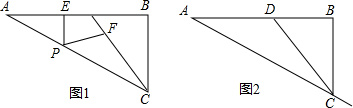
分析 (1)BC=PE+PF.如图1,过点P作PH⊥BC于点H,所以∠PHB=90°,由PE⊥AD,得到∠PEB=90°,因为∠ABC=90°,所以四边形BEPH为矩形,得到PE=BH,AB∥PH,再证明△PCH≌△CPF,得到CH=PF,由BC=BH+CH,所以BC=PE+PF.
(2)根据题意补全图形,猜想并得到结论:AB=PE-PF.
解答 解:(1)BC=PE+PF.
证明:如图1,过点P作PH⊥BC于点H,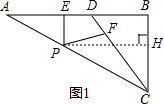
∴∠PHB=90°,
∵PE⊥AD,
∴∠PEB=90°,
∵∠ABC=90°,
∴四边形BEPH为矩形,
∴PE=BH,AB∥PH,
∴∠A=∠CPH,
∵AD=CD,
∴∠A=∠DCA,
∴∠CPH=∠DCA,
∵PF⊥CD,
∴∠PHC=∠PFC=90°,
在△PCH和△CPF中,
$\left\{\begin{array}{l}{∠CPH=∠DCA}\\{∠PHC=∠PFC}\\{PC=PC}\end{array}\right.$,
∴△PCH≌△CPF,
∴CH=PF,
∵BC=BH+CH,
∴BC=PE+PF.
(2)补全图形,如图2所示,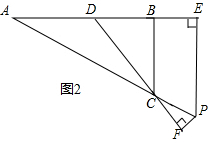
结论:BC=PE-PF.
点评 本题考查了矩形的性质、全等三角形的判定定理和性质定理,解决本题的关键是作出辅助线,证明三角形全等.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
16.某校为了充实师资力量,决定招聘一位数学教师,对应聘者进行笔试和试讲两项综合考核,根据重要性,笔试成绩占30%,试讲成绩占70%,应聘者王晓、张会两人的得分如下表,如果你是校长,你会录用谁?请说明理由.
| 姓名 | 笔试 | 试讲 |
| 王晓 | 81分 | 95分 |
| 张会 | 90分 | 82分 |
17.已知:x+y=8,xy=12,则x2+y2的值是( )
| A. | 40 | B. | 48 | C. | 80 | D. | 88 |
18.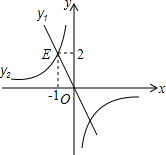 如图,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围是( )
如图,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围是( )
 如图,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围是( )
如图,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围是( )| A. | x<-1 | B. | -1<x<0 | C. | x>1 | D. | 0<x<1 |
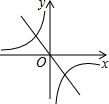
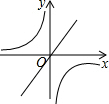
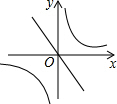
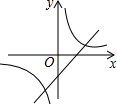
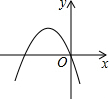 如果二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=$\frac{b}{x}$在同一坐标系中的图象大致是( )
如果二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=$\frac{b}{x}$在同一坐标系中的图象大致是( )