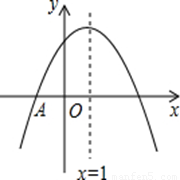题目内容
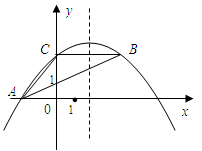
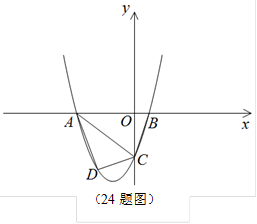
(8分)如图,抛物线 与
与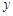 轴交于点
轴交于点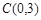 ,与
,与 轴交于
轴交于 ,B两点(点A在点B的右侧),过C作直线
,B两点(点A在点B的右侧),过C作直线 ,与抛物线相交于点
,与抛物线相交于点 ,与对称轴交于点N,点
,与对称轴交于点N,点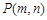 为直线
为直线 上的一个动点,过P作
上的一个动点,过P作 轴的垂线交抛物线于点G,设线段PG的长度为
轴的垂线交抛物线于点G,设线段PG的长度为

(1)求该抛物线的函数解析式
(2)当0< <5时,请用含
<5时,请用含 的代数式表示
的代数式表示 ,求出
,求出 的最大值
的最大值
(3)是否存在这样的点P,使以M,N,P,G为顶点的四边形是平行四边形,若存在,请求出点P的坐标;若存在,请说明理由。
(1) (2)
(2) (3) P的坐标
(3) P的坐标
解析试题分析:
解:
(1)
(2)直线 :
: 又
又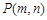 ∴
∴

0< <5时
<5时 
∴ 时,
时, 有最大值
有最大值
(1)顶点M(2,-1),N(2,5),则MN=6
∵PG∥MN ∴只要PG=MN=6就能证明四边形为平行四边形
当P在G的上面时 =6,解得
=6,解得 ,
, (舍去)
(舍去)
当P在G的下面时-( )=6解得
)=6解得 ,
, 时
时
∴P的坐标
考点:二次函数的求法
点评:此类试题的解答主要是分析二次函数的顶点公式,以及求法,几种做法。

练习册系列答案
相关题目

 在
在 在
在 .
.

 1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:
1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论: ;④3≤n≤4中,
;④3≤n≤4中,