Question

（2013年浙江义乌3分）如图，抛物线y=ax²+bx+c与x轴交于点A（1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点），则下列结论：

①当x＞3时，y＜0；②3a+b＞0；③；④3≤n≤4中，

正确的是【    】

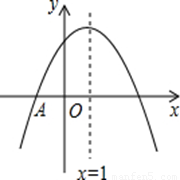
A．①②　　　　B．③④　 　C．①④　　 D．①③

 

Answer 1

【答案】

D。

【解析】①∵抛物线y=ax²+bx+c与x轴交于点A（-1，0），对称轴直线是x=1，

∴该抛物线与x轴的另一个交点的坐标是（3，0），

∴根据图示知，当x＞3时，y＜0。故①正确。

②根据图示知，抛物线开口方向向下，则a＜0。

∵对称轴，∴b=-2a。

∴3a+b=3a-2a=a＜0，即3a+b＜0。故②错误。

③∵抛物线与x轴的两个交点坐标分别是（－1，0），（3，0），∴－1×3=-3。

∴，则。

∵抛物线与y轴的交点在（0，2）、（0，3）之间（包含端点），∴2≤c≤3。

∴，即。故③正确。

④根据题意知，，

∵2≤c≤3，∴，即。故④错误。

综上所述，正确的说法有①③。故选D。

考点：二次函数图象与系数的关系。