题目内容
2.一个菱形两条对角线的和是12cm,面积是16cm2,求菱形的周长.分析 由对角线的和及对角线的乘积可分别求解对角线的长,进而在直角三角形中求解菱形的边长,则可求其周长.
解答 解:如图
由题意可得,BD+AC=12,$\frac{1}{2}$•BD•AC=16,
解得:BD=4,AC=8,
∵四边形ABCD是菱形,
∴OA=OC=4,OB=OD=2,
在Rt△AOB中,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∴菱形的周长=4AB=8$\sqrt{5}$.
点评 本题考查了菱形的性质、勾股定理;熟练掌握菱形的性质,由勾股定理求出AB是解决问题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
11. 如图,∠ACB=90°,CD⊥AB,垂足为D,则点A到CD的距离可用线段( )的长度来表示.
如图,∠ACB=90°,CD⊥AB,垂足为D,则点A到CD的距离可用线段( )的长度来表示.
 如图,∠ACB=90°,CD⊥AB,垂足为D,则点A到CD的距离可用线段( )的长度来表示.
如图,∠ACB=90°,CD⊥AB,垂足为D,则点A到CD的距离可用线段( )的长度来表示.| A. | AC | B. | AD | C. | AB | D. | CD |
 是
是  的弦,
的弦,  是
是  的切线,
的切线,  为切点,
为切点,  经过圆心,若
经过圆心,若  ,则
,则  的大小等于( )
的大小等于( ) 
 B.
B. 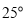 C.
C.  D.
D. 
 平行四边形各内角平分线所围成的四边形是什么图形?请证明你的观点.
平行四边形各内角平分线所围成的四边形是什么图形?请证明你的观点. 如图是李峰家一块平行四边形花圃,周长为36cm,且DE⊥AB,DF⊥BC,DE=5,DF=7,求花圃的面积.
如图是李峰家一块平行四边形花圃,周长为36cm,且DE⊥AB,DF⊥BC,DE=5,DF=7,求花圃的面积.