题目内容
 已知线段AB=6厘米,延长AB到点C,使得BC=
已知线段AB=6厘米,延长AB到点C,使得BC=| 1 |
| 2 |
考点:两点间的距离
专题:
分析:先根据线段AB=6厘米,BC=
AB得出BC的长,故可得出AC的长,再根据M是AC的中点求出AM的长,根据MB=AB-AM即可得出结论.
| 1 |
| 2 |
解答:解:∵AB=6厘米,BC=
AB,
∴BC=3厘米.
∴AC=AB+BC=6+3=9(厘米),
∵M是AC的中点,
∴AM=
AC=
×9=4.5(厘米),
∴MB=AB-AM=6-4.5=1.5(厘米),
故MB的长度是1.5厘米.
| 1 |
| 2 |
∴BC=3厘米.
∴AC=AB+BC=6+3=9(厘米),
∵M是AC的中点,
∴AM=
| 1 |
| 2 |
| 1 |
| 2 |
∴MB=AB-AM=6-4.5=1.5(厘米),
故MB的长度是1.5厘米.
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
下列说法中,不正确的是( )
| A、单项式-x的系数是-1,次数是1 |
| B、单项式xy2z3的系数是1,次数是6 |
| C、单项式-32ab3的次数是6 |
| D、xy-3x+2是二次三项式 |
下列说法:①两点确定一条直线;②射线AB和射线BA是同一条射线;③相等的角是对顶角;④三角形任意两边和大于第三边的理由是两点之间线段最短.正确的是( )
| A、①③④ | B、①②④ |
| C、①④ | D、②③④ |
已知线段AB=8cm,在直线AB上有一点C,且BC=4cm,点M是线段AC的中点,则线段AM的长为( )
| A、2cm |
| B、4cm |
| C、2cm或6cm |
| D、4cm或6cm |
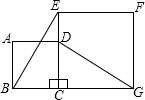 如图所示,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE,DG.
如图所示,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE,DG.