题目内容
图1为全体奇数排成的数表,用十字框任意框出5个数,记框内中间这个数为a(如图2).
(1)请用含a的代数式表示框内的其余4个数;
(2)框内的5个数之和能等于2015,2020吗?若不能,请说明理由;若能,请求出这5个数中最小的一个数,并写出最小的这个数在图1数表中的位置.(自上往下第几行,自左往右的第几个)

(1)请用含a的代数式表示框内的其余4个数;
(2)框内的5个数之和能等于2015,2020吗?若不能,请说明理由;若能,请求出这5个数中最小的一个数,并写出最小的这个数在图1数表中的位置.(自上往下第几行,自左往右的第几个)

考点:一元一次方程的应用
专题:
分析:(1)上下相邻的数相差18,左右相邻的数相差是2,所以可用a表示;
(2)根据等量关系:框内的5个数之和能等于2015,2020,分别列方程分析求解.
(2)根据等量关系:框内的5个数之和能等于2015,2020,分别列方程分析求解.
解答:解:(1)设中间的数是a,则a的上一个数为a-18,下一个数为a+18,前一个数为a-2,后一个数为a+2;
(2)设中间的数是a,依题意有
5a=2015,
a=403,符合题意,
这5个数中最小的一个数是a-18=403-18=385,
2n-1=385,解得n=193,
193÷9=21…4,
最小的这个数在图1数表中的位置第22排第4列.
5a=2020,
a=404,
404是偶数,不合题意舍去;
即十字框中的五数之和不能等于2020,能等于2015.
(2)设中间的数是a,依题意有
5a=2015,
a=403,符合题意,
这5个数中最小的一个数是a-18=403-18=385,
2n-1=385,解得n=193,
193÷9=21…4,
最小的这个数在图1数表中的位置第22排第4列.
5a=2020,
a=404,
404是偶数,不合题意舍去;
即十字框中的五数之和不能等于2020,能等于2015.
点评:本题考查一元一次方程的应用,关键是看到表格中中间位置的数和四周数的关系,最后可列出方程求解.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
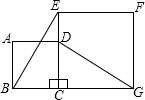 如图所示,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE,DG.
如图所示,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE,DG.(1)观察猜想线段BE与DG之间的大小关系,并证明你的结论;
(2)观察猜想直线BE与直线DG之间的位置关系,并证明你的结论.
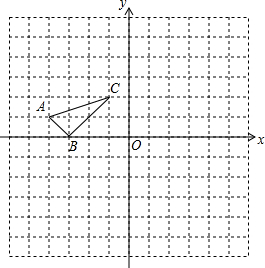
 有理数a、b在数轴上的位置如图所示,则下列各式中错误的是( )
有理数a、b在数轴上的位置如图所示,则下列各式中错误的是( )| A、b<0<a |
| B、|b|>|a| |
| C、a+b>0 |
| D、ab<0 |
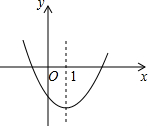 二次函数y=ax2+bx+c图象如图,下列正确的个数为( )
二次函数y=ax2+bx+c图象如图,下列正确的个数为( )①abc>0;②2a-3c<0;③2a+b>0;④ax2+bx+c=0有两个实数解x1,x2,且x1+x2<0; ⑤9a+3b+c>0;⑥当x<1时,y随x增大而减小.
| A、2 | B、3 | C、4 | D、5 |
已知sinα<0.5,那么锐角α的取值范围是( )
| A、60°<α<90° |
| B、30°<α<90° |
| C、0°<α<60° |
| D、0°<α<30° |
 每个小正方形边长都为1个单位长度.
每个小正方形边长都为1个单位长度. 如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴上的一动点,连接CD,DE,以CD,DE为边作?CDEF.
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴上的一动点,连接CD,DE,以CD,DE为边作?CDEF.