题目内容
15.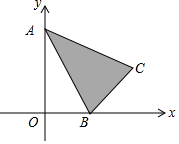 如图,已知△ABC的顶点坐标分别为A(0,2)、B(1,0)、C(2,1),若二次函数y=x2+bx+1的图象与阴影部分(含边界)一定有公共点,则实数b的取值范围是( )
如图,已知△ABC的顶点坐标分别为A(0,2)、B(1,0)、C(2,1),若二次函数y=x2+bx+1的图象与阴影部分(含边界)一定有公共点,则实数b的取值范围是( )| A. | b≤-2 | B. | b<-2 | C. | b≥-2 | D. | b>-2 |
分析 对称轴x=-$\frac{b}{2}$≤1时,二次函数y=x2+bx+1的图象与阴影部分(含边界)一定有公共点.
解答 解:抛物线y=x2+bx+1与y轴的交点为(0,1)
∵C(2,1),
∴对称轴x=-$\frac{b}{2}$≤1时,二次函数y=x2+bx+1的图象与阴影部分(含边界)一定有公共点,
∴b≥-2,
故选:C.
点评 本题考查了二次函数图象与系数的关系.解题时,利用了二次函数图象上点的坐标特征来求b的取值范围.

练习册系列答案
相关题目
6.某服装店销售A、B两种品牌服装,且平均每月销售80件,已知这两种品牌服装的成本和售价如下表所示:
设该服装店每月销售的A品牌服装x件,平均每月获得的总利润为y元.
(1)写出y与x的函数关系式;
(2)如果该服装店平均每月投入的总成本不超过7500元,不考虑其他因素,那么当A、B两种品牌服装各销售多少件时,该服装店平均每月的总利润最大?并求出这个最大利润.
| A | B | |
| 成本(万元/件) | 100 | 80 |
| 售价(万元/件) | 170 | 120 |
(1)写出y与x的函数关系式;
(2)如果该服装店平均每月投入的总成本不超过7500元,不考虑其他因素,那么当A、B两种品牌服装各销售多少件时,该服装店平均每月的总利润最大?并求出这个最大利润.
7.若一次函数y=(a+1)x+a的图象过第一、三、四象限,则二次函数y=ax2-ax( )
| A. | 有最大值$\frac{a}{4}$ | B. | 有最大值-$\frac{a}{4}$ | C. | 有最小值$\frac{a}{4}$ | D. | 有最小值-$\frac{a}{4}$ |
5.云南某特产公司组织20辆汽车装运三七、普洱茶、鲜花饼三种特产去省外销售,按计划20辆汽车都要装运,每辆汽车只能运送同一种特产,且必须装满,根据下表提供的信息,解答以下问题;
若装运三七的车辆数为x,装运鲜花饼的车辆数比装运三七的车辆数的2倍少1辆,假设三种特产的总利润为y万元.
(1)求y与x的函数关系式;
(2)若装运普洱茶的汽车不超过6辆,求总利润最大时,装运各种特产的车辆数及总利润最大值.
| 特产名称 | 三七 | 普洱茶 | 鲜花饼 |
| 每辆汽车运载量(吨) | 8 | 6 | 5 |
| 每吨特产利润(万元) | 1.2 | 1.6 | 1 |
(1)求y与x的函数关系式;
(2)若装运普洱茶的汽车不超过6辆,求总利润最大时,装运各种特产的车辆数及总利润最大值.
 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时血液中含药量为每毫升3微克,每毫升血液中含药量y微克随时间x小时主变化如图所示,当成人按规定剂是服药后,
某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时血液中含药量为每毫升3微克,每毫升血液中含药量y微克随时间x小时主变化如图所示,当成人按规定剂是服药后,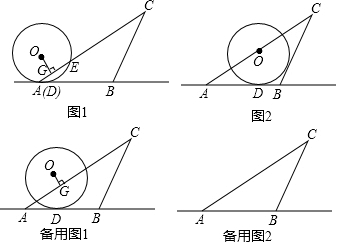
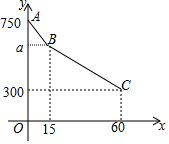 周末,小军在医院里照顾奶奶输液,小军问:“按照这样的输液速度,多少时间能结束输液?”护上答:“75分钟.”15分钟后,小军减慢了输液的速度,60分钟后,小军发现还剩有300毫升药液,剩下待输药液y(毫升)与输液时间x(分钟)的函数关系如图所示.
周末,小军在医院里照顾奶奶输液,小军问:“按照这样的输液速度,多少时间能结束输液?”护上答:“75分钟.”15分钟后,小军减慢了输液的速度,60分钟后,小军发现还剩有300毫升药液,剩下待输药液y(毫升)与输液时间x(分钟)的函数关系如图所示. 小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地280米.小明登上山顶立即沿原路按某一速度匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程y1(米)、y2(米)与小明出发的时间x(分)的函数关系如图.
小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地280米.小明登上山顶立即沿原路按某一速度匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程y1(米)、y2(米)与小明出发的时间x(分)的函数关系如图.