题目内容
 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船c的求救信号.已知A、B两船相距100(
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船c的求救信号.已知A、B两船相距100(| 3 |
(1)分别求出A与C,A与D之间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距观测点D处200海里范围内有暗礁.若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?(参考数据:
| 2 |
| 3 |
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)作CE⊥AB于点E,则∠ABC=45°,∠BAC=60°,设AE=x海里,在Rt△AEC中,CE=AE•tan60°,在Rt△BCE中,BE=CE=
x,由AE+BE=x+
x=100(3+
)求出x的值,再根据AC=2x得出AC的值,在△ACD中,由∠DAC=60°,∠ADC=75°得出∠ACD=45°.过点D作DF⊥AC于点F,设AF=y,则DF=CF=
y,根据AC=y+
y=200
求出y的值,故可得出AD的长,进而得出结论;
(2)根据(1)中的结论得出DF的长,再与200相比较即可.
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
(2)根据(1)中的结论得出DF的长,再与200相比较即可.
解答: 解:(1)作CE⊥AB于点E,则∠ABC=45°,∠BAC=60°,设AE=x海里,
解:(1)作CE⊥AB于点E,则∠ABC=45°,∠BAC=60°,设AE=x海里,
∵在Rt△AEC中,CE=AE•tan60°=
x,
在Rt△BCE中,BE=CE=
x,
∴AE+BE=x+
x=100(3+
),解得x=100
,
∴AC=2x=200
.
在△ACD中,
∵∠DAC=60°,∠ADC=75°,
∴∠ACD=45°.
过点D作DF⊥AC于点F,设AF=y,则DF=CF=
y,
∴AC=y+
y=200
,解得y=100(3-
),
∴AD=2x=200(3-
).
答:A与C之间的距离AC为200
海里,A与D之间的距离AD为200(3-
)海里;
(2)∵由(1)可知,DF=
AF=
×100(3-
)≈219.
∵219>200,
∴巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险.
 解:(1)作CE⊥AB于点E,则∠ABC=45°,∠BAC=60°,设AE=x海里,
解:(1)作CE⊥AB于点E,则∠ABC=45°,∠BAC=60°,设AE=x海里,∵在Rt△AEC中,CE=AE•tan60°=
| 3 |
在Rt△BCE中,BE=CE=
| 3 |
∴AE+BE=x+
| 3 |
| 3 |
| 3 |
∴AC=2x=200
| 3 |
在△ACD中,
∵∠DAC=60°,∠ADC=75°,
∴∠ACD=45°.
过点D作DF⊥AC于点F,设AF=y,则DF=CF=
| 3 |
∴AC=y+
| 3 |
| 3 |
| 3 |
∴AD=2x=200(3-
| 3 |
答:A与C之间的距离AC为200
| 3 |
| 3 |
(2)∵由(1)可知,DF=
| 3 |
| 3 |
| 3 |
∵219>200,
∴巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险.
点评:本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图所示,其中是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
下列各组线段中
(1)m2-n2、2mn、m2+n2(m,n为正整数,且m>n);
(2)9,12,15;
(3)7,24,25;
(4)32,42,52;
(5)
、
、
;
其中可以构成直角三角形的有( )组.
(1)m2-n2、2mn、m2+n2(m,n为正整数,且m>n);
(2)9,12,15;
(3)7,24,25;
(4)32,42,52;
(5)
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
其中可以构成直角三角形的有( )组.
| A、2 | B、3 | C、4 | D、5 |
已知一个三角形的三边长分别为a、b、c,且它们满足(a+b)2-c2=2ab,则该三角形的形状为( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法确定 |
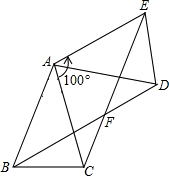 如图,在△ABC中,已知AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD,CE交于点F.
如图,在△ABC中,已知AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD,CE交于点F.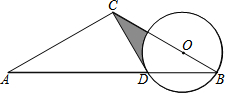 如图,△ABC中,AC=BC,以BC上一点O为圆心,OB为半径作⊙O交AB于点D.已知经过点D的⊙O切线恰好经过点C.
如图,△ABC中,AC=BC,以BC上一点O为圆心,OB为半径作⊙O交AB于点D.已知经过点D的⊙O切线恰好经过点C. 用长为8米的铝合金制成如图所示的窗框,若设窗框的宽为x米,窗户的透光面积为S平方米,则S关于x的函数关系式为
用长为8米的铝合金制成如图所示的窗框,若设窗框的宽为x米,窗户的透光面积为S平方米,则S关于x的函数关系式为
 一个几何体由多个小立方块搭成,如图是从它的上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.请画出从正面,左面看它的形状图.
一个几何体由多个小立方块搭成,如图是从它的上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.请画出从正面,左面看它的形状图.