题目内容
10．化简$\sqrt{{x}^{2}+6x+9}$+$\sqrt{{x}^{2}-2x+1}$的结果为-2x-2或4或2x+2．．分析 根据x的取值范围不同进而分别化简得出即可．
解答 解：原式=$\sqrt{（x+3）^{2}}$+$\sqrt{（x-1）^{2}}$=|x+3|+|x-1|，
当x＜-3时，原式=-2x-2，
当-3≤x≤1时，原式=4，
当x＞1时，原式=2x+2．
故答案为：-2x-2或4或2x+2．
点评 此题主要考查了二次根式的化简，正确利用分类讨论得出是解题关键．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
20．先阅读下列一段文字，然后解答问题：
某运输部门规定：办理托运，当一种物品的重量不超过16千克时，需付基础费30元和保险费a元：为限制过重物品的托运，当一件物品超过16千克时，除了付以上基础费和保险费外，超过部分每千克还需付b元超重费．设某件物品的重量为x千克．
（1）当x≤16时，支付费用为a+30元（用含a的代数式表示）；当x≥16时，支付费用为a+30+（x-16）b元（用含x和a、b的代数式表示）；
（2）甲、乙两人各托运一件物晶，物品重量和支付费用如下表所示
①试根据以上提供的信息确定a，b的值．
②试问在物品可拆分的情况下，用不超过105元的费用能否托运50千克物品？若能，请设计出其中一种托运方案，并求出托运费用；若不能，请说明理由．
某运输部门规定：办理托运，当一种物品的重量不超过16千克时，需付基础费30元和保险费a元：为限制过重物品的托运，当一件物品超过16千克时，除了付以上基础费和保险费外，超过部分每千克还需付b元超重费．设某件物品的重量为x千克．
（1）当x≤16时，支付费用为a+30元（用含a的代数式表示）；当x≥16时，支付费用为a+30+（x-16）b元（用含x和a、b的代数式表示）；
（2）甲、乙两人各托运一件物晶，物品重量和支付费用如下表所示
| 物品重量（千克） | 支付费用（元） |
| 18 | 38 |
| 25 | 53 |
②试问在物品可拆分的情况下，用不超过105元的费用能否托运50千克物品？若能，请设计出其中一种托运方案，并求出托运费用；若不能，请说明理由．
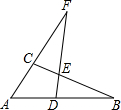如图，△ABC中，D，E分别是AB和BC上的点，直线DE与AC的延长线交于点F，且AD•AB=AC•AF．求证：
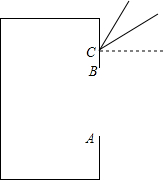某地在一年中阳光与地面的最大角为60°，最小角为30°，当地的某一新建住宅区的住户准备统一在向阳的一边设计统一高度的窗，并在这些窗上方做一块“遮阳蓬”，如图所示．已知窗的统一高度AB为2米，试用你所学的知识，计算“遮阳蓬”CD应从窗的上方多高的点C伸出，伸出多长才能使房间内“冬暖夏凉”？
求阴影部分的面积．
在△ABC中，E、F分别为边AB、AC的中点，G为线段EF上一点，记△ABC、△AGC、△ABG、△GBC面积分别为S、S1、S2、S3，已知S1=λ1S，S2=λ2S，S3=λ3S，且λ3=2λ1，则$\frac{1}{λ_1}+\frac{2}{λ_2}+\frac{3}{λ_3}$=18．
2015年5月中旬，中国和俄罗斯海军在地中海海域举行了代号为“海上联合-2015（1）”的联合军事演习，这是中国第一次地中海举行军事演习，也是这个海军距本土最远的一次军演，某天，“临沂舰”、“潍坊舰”两舰同时从A、B两个港口出发，均沿直线匀速驶向演习目标地海岛C，两舰艇都到达C岛后演习第一阶段结束，已知B刚位于A港、C岛之间，且A、B、C在一条直线上，如图所示，l临、l潍分别表示“临沂舰”、“潍坊舰”离B港的距离行驶时间x（h）变化的图象．