题目内容
15.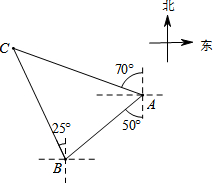 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )| A. | 10$\sqrt{2}$海里 | B. | 10$\sqrt{3}$海里 | C. | 10$\sqrt{6}$海里 | D. | 20$\sqrt{6}$海里 |
分析 作BD⊥AC于点D,在直角△ABD中,利用三角函数求得BD的长,然后在直角△BCD中,利用三角函数即可求得BC的长.
解答  解:作BD⊥AC于点D.
解:作BD⊥AC于点D.
∵∠CBA=25°+50°=75°,
∴∠CAB=(90°-70°)+(90°-50°)=20°+40°=60°,
∠ABD=30°,
∴∠CBD=75°-30°=45°.
在直角△ABD中,BD=AB•sin∠CAB=20×sin60°=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$.
在直角△BCD中,∠CBD=45°,
则BC=$\sqrt{2}$BD=10$\sqrt{3}$×$\sqrt{2}$=10$\sqrt{6}$(海里).
故选C.
点评 本题考查的是解直角三角形的应用-方向角问题,正确求得∠CBD以及∠CAB的度数是解决本题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
9.若一次函数y=ax+b的图象经过第一、二、四象限,则下列不等式中总是成立的是( )
| A. | a2+b>0 | B. | a-b>0 | C. | a2-b>0 | D. | a+b>0 |
6.代数式(22+1)(24+1)(28+1)…(232+1)+1的个位数是( )
| A. | 4 | B. | 0 | C. | 6 | D. | 2 |
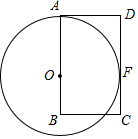 如图,矩形ABCD中,AB=9,O是AB边上一点,以O为圆心,OA为半径画圆与边CD相切于点F,与BC相交于点E,若EC=2,则⊙O的半径为5.
如图,矩形ABCD中,AB=9,O是AB边上一点,以O为圆心,OA为半径画圆与边CD相切于点F,与BC相交于点E,若EC=2,则⊙O的半径为5. 已知:直线L和L外一点P,根据所学的“用尺规作一个角等于已知角”
已知:直线L和L外一点P,根据所学的“用尺规作一个角等于已知角”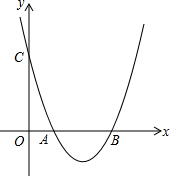 已知二次函数y=a(x-1)(x-3)(a>0)的图象与x轴交于A、B两点(A左B右),与y轴交于C点(0,3).P为x轴下方二次函数y=a(x-1)(x-3)(a>0)图象上一点,P点横坐标为m.
已知二次函数y=a(x-1)(x-3)(a>0)的图象与x轴交于A、B两点(A左B右),与y轴交于C点(0,3).P为x轴下方二次函数y=a(x-1)(x-3)(a>0)图象上一点,P点横坐标为m. 【阅读理解】我们知道,当a>0且b>0时,($\sqrt{a}$-$\sqrt{b}$)2≥0,所以a-2$\sqrt{ab}$+≥0,从而a+b≥2$\sqrt{ab}$(当a=b时取等号),
【阅读理解】我们知道,当a>0且b>0时,($\sqrt{a}$-$\sqrt{b}$)2≥0,所以a-2$\sqrt{ab}$+≥0,从而a+b≥2$\sqrt{ab}$(当a=b时取等号),