题目内容
7.某花圃销售一批名贵花卉,平均每天可售出20盆,每盆盈利40元,为了增加盈利并尽快减少库存,花圃决定采取适当的降价措施,经调查发现,如果每盆花卉每降1元,花圃平均每天可多售出2盆.(1)若花圃平均每天要盈利1200元,每盆花卉应降价多少元?
(2)每盆花卉降低多少元时,花圃平均每天盈利最多,是多少?
分析 (1)利用每盆花卉每天售出的盆数×每盆的盈利=每天销售这种花卉的利润,列出方程解答即可;
(2)利用每盆花卉每天售出的盆数×每盆的盈利=每天销售这种花卉的利润y,列出函数关系式解答即可.
解答 解:(1)设每盆花卉应降价x元,根据题意可得:
(40-x)(20+2x)=1200,
解得:x1=10,x2=20,
∵为了增加盈利并尽快减少库存,
∴x=20,
答:若花圃平均每天要盈利1200元,每盆花卉应降价20元;
(2)设每盆花卉降低x元,花圃每天盈利y元,则
y=(40-x)(20+2x)
=-2x2+60x+800
=-2(x-15)2+1250,
由$\left\{\begin{array}{l}{x≥0}\\{40-x>0}\end{array}\right.$,
解得:0≤x<40,
故当x=15时,y最大=1250,
答:每盆花卉降低15元时,花圃每天盈利最多为1250元.
点评 此题主要考查了一元二次方程的应用以及二次函数的应用,正确得出等量关系是解题关键.

练习册系列答案
相关题目
15.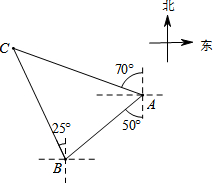 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )| A. | 10$\sqrt{2}$海里 | B. | 10$\sqrt{3}$海里 | C. | 10$\sqrt{6}$海里 | D. | 20$\sqrt{6}$海里 |
16. 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )
 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )| A. | 圆锥 | B. | 三棱锥 | C. | 四棱锥 | D. | 四棱柱 |
 如图,在等边△ABC中,AB=4,P、M、N分别是BC、CA、AB边上动点,则PM+MN的最小值是2$\sqrt{3}$.
如图,在等边△ABC中,AB=4,P、M、N分别是BC、CA、AB边上动点,则PM+MN的最小值是2$\sqrt{3}$.