��Ŀ����
�Ķ����в��ϣ�
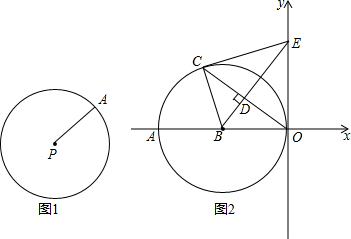
��ͼ1��Բ�ĸ����ƽ���ڣ��߶�PA�����̶���һ���˵�P��תһ�ܣ���һ���˵�A���γɵ�ͼ�ν���Բ������˵����ij��������ڶ��������е���ͬһ��Բ�ϣ�Բ����P��a��b�����뾶Ϊr��Բ�ķ��̿���дΪ����x-a��2+��y-b��2=r2���磺Բ����P��2��-1�����뾶Ϊ5��Բ����Ϊ����x-2��2+��y+1��2=25
��1����գ�
����A��3��0��ΪԲ�ģ�1Ϊ�뾶��Բ�ķ���Ϊ ��
����B��-1��-2��ΪԲ�ģ�
Ϊ�뾶��Բ�ķ���Ϊ ��
��2���������ϲ��Ͻ���������⣺
��ͼ2����B��-6��0��ΪԲ�ĵ�Բ��y��������ԭ�㣬C�ǡ�B��һ�㣬����OC����BD��OC����ΪD���ӳ�BD��y���ڵ�E����֪sin��AOC=
��
������EC��֤��EC�ǡ�B�����ߣ�
����BE���Ƿ����һ��P��ʹPB=PC=PE=PO�������ڣ���P�����꣬��д����PΪԲ�ģ���PBΪ�뾶�ġ�P�ķ��̣��������ڣ�˵�����ɣ�
��ͼ1��Բ�ĸ����ƽ���ڣ��߶�PA�����̶���һ���˵�P��תһ�ܣ���һ���˵�A���γɵ�ͼ�ν���Բ������˵����ij��������ڶ��������е���ͬһ��Բ�ϣ�Բ����P��a��b�����뾶Ϊr��Բ�ķ��̿���дΪ����x-a��2+��y-b��2=r2���磺Բ����P��2��-1�����뾶Ϊ5��Բ����Ϊ����x-2��2+��y+1��2=25

��1����գ�
����A��3��0��ΪԲ�ģ�1Ϊ�뾶��Բ�ķ���Ϊ
����B��-1��-2��ΪԲ�ģ�
| 3 |
��2���������ϲ��Ͻ���������⣺
��ͼ2����B��-6��0��ΪԲ�ĵ�Բ��y��������ԭ�㣬C�ǡ�B��һ�㣬����OC����BD��OC����ΪD���ӳ�BD��y���ڵ�E����֪sin��AOC=
| 3 |
| 5 |
������EC��֤��EC�ǡ�B�����ߣ�
����BE���Ƿ����һ��P��ʹPB=PC=PE=PO�������ڣ���P�����꣬��д����PΪԲ�ģ���PBΪ�뾶�ġ�P�ķ��̣��������ڣ�˵�����ɣ�
���㣺Բ���ۺ���,���������ε�����,���ɶ���,��������,Բ�ܽǶ���,���ߵ��ж�
ר�⣺�ۺ���,�Ķ���
��������1�������Ķ������еĶ�����⣻
��2���ٸ��ݴ���������BD��OC�õ�CD=OD����BE��ֱƽ��OC���ٸ����߶δ�ֱƽ���ߵ����ʵ�EO=EC�����EOC=��ECO��
���ϡ�BOC=��BCO���á�BOE=��BCE=90�㣬Ȼ��������ߵ��ж������õ�EC�ǡ�B�����ߣ�
���ɡ�BOE=��BCE=90�㣬����Բ�ܽǶ����õ�C�͵�Oż����BEΪֱ����Բ�ϣ�����P��ΪBE���е�ʱ������PB=PC=PE=PO������ͬ�ǵ������ȵá�BOE=��AOC����sin��BOE=sin��AOC=
����Rt��BOE�У��������ҵĶ�������BE=10�����ù��ɶ��������OE=8����E������Ϊ��0��8�������ǵõ��߶�AB���е�P������Ϊ��-3��4����PB=5��Ȼ��д����P��-3��4��ΪԲ�ģ���5Ϊ�뾶�ġ�P�ķ��̣�
��2���ٸ��ݴ���������BD��OC�õ�CD=OD����BE��ֱƽ��OC���ٸ����߶δ�ֱƽ���ߵ����ʵ�EO=EC�����EOC=��ECO��
���ϡ�BOC=��BCO���á�BOE=��BCE=90�㣬Ȼ��������ߵ��ж������õ�EC�ǡ�B�����ߣ�
���ɡ�BOE=��BCE=90�㣬����Բ�ܽǶ����õ�C�͵�Oż����BEΪֱ����Բ�ϣ�����P��ΪBE���е�ʱ������PB=PC=PE=PO������ͬ�ǵ������ȵá�BOE=��AOC����sin��BOE=sin��AOC=
| 3 |
| 5 |
�����1���⣺����A��3��0��ΪԲ�ģ�1Ϊ�뾶��Բ�ķ���Ϊ��x-3��2+y2=1��
����B��-1��-2��ΪԲ�ģ�
Ϊ�뾶��Բ�ķ���Ϊ��x+1��2+��y+2��2=3��
�ʴ�Ϊ��x-3��2+y2=1����x+1��2+��y+2��2=3��
 ��1����֤������BD��OC��
��1����֤������BD��OC��
��CD=OD��
��BE��ֱƽ��OC��
��EO=EC��
���EOC=��ECO��
��BO=BC��
���BOC=��BCO��
���EOC+��BOC=��ECO+��BCO��
���BOE=��BCE=90�㣬
��BC��CE��
��EC�ǡ�B�����ߣ�
�ڴ��ڣ�
�ߡ�BOE=��BCE=90�㣬
���C�͵�Oż����BEΪֱ����Բ�ϣ�
�൱P��ΪBE���е�ʱ������PB=PC=PE=PO��
��B��������-6��0����
��OB=6��
�ߡ�AOC+��DOE=90�㣬��DOE+��BEO=90�㣬
���BEO=��AOC��
��sin��BEO=sin��AOC=
��
��Rt��BOE��sin��BEO=
��
��
=
��
��BE=10��
��OE=
=8��
��E��������0��8����
���߶�AB���е�P������Ϊ��-3��4����PB=5��
����P��-3��4��ΪԲ�ģ���5Ϊ�뾶�ġ�P�ķ���Ϊ��x+3��2+��y-4��2=25��
����B��-1��-2��ΪԲ�ģ�
| 3 |
�ʴ�Ϊ��x-3��2+y2=1����x+1��2+��y+2��2=3��
 ��1����֤������BD��OC��
��1����֤������BD��OC����CD=OD��
��BE��ֱƽ��OC��
��EO=EC��
���EOC=��ECO��
��BO=BC��
���BOC=��BCO��
���EOC+��BOC=��ECO+��BCO��
���BOE=��BCE=90�㣬
��BC��CE��
��EC�ǡ�B�����ߣ�
�ڴ��ڣ�
�ߡ�BOE=��BCE=90�㣬
���C�͵�Oż����BEΪֱ����Բ�ϣ�
�൱P��ΪBE���е�ʱ������PB=PC=PE=PO��
��B��������-6��0����
��OB=6��
�ߡ�AOC+��DOE=90�㣬��DOE+��BEO=90�㣬
���BEO=��AOC��
��sin��BEO=sin��AOC=
| 3 |
| 5 |
��Rt��BOE��sin��BEO=
| OB |
| BE |
��
| 6 |
| BE |
| 3 |
| 5 |
��BE=10��
��OE=
| BE2-OB2 |
��E��������0��8����
���߶�AB���е�P������Ϊ��-3��4����PB=5��
����P��-3��4��ΪԲ�ģ���5Ϊ�뾶�ġ�P�ķ���Ϊ��x+3��2+��y-4��2=25��
������������Բ���ۺ��⣺�������մ������������ߵ��ж�������Բ�ܽǶ����͵��������ε����ʣ��Ķ���������Ҳ�DZ��⿼����ص㣻������������Ǻ����Ķ�����ɶ������м��μ��㣮

��ϰ��ϵ�д�
�����Ŀ
ijͬѧ�����һöӲ���������20�Σ���12�γ��ַ��棬��ô������ֵ�Ƶ���ǣ�������
| A��0.12 | B��0.4 |
| C��0.8 | D��0.6 |
 ��ƽ���ı���ABCD�У�����ABC��AC���ۣ�ʹ��B����B�䴦��A B���CD�ཻ�ڵ�O����֤��OA=OC��
��ƽ���ı���ABCD�У�����ABC��AC���ۣ�ʹ��B����B�䴦��A B���CD�ཻ�ڵ�O����֤��OA=OC��