题目内容
若x是实数，已知M=3x2-5x+2，N=2x2-3x+1，则M，N的大小关系是（ ）
| A、M＞N | B、M＜N |
| C、M=N | D、M≥N |
考点：因式分解-运用公式法,非负数的性质：偶次方
专题：
分析：直接得出M-N的值再利用配方法得出M，N的大小关系．
解答：解：∵M=3x2-5x+2，N=2x2-3x+1，
∴M-N=（3x2-5x+2）-（2x2-3x+1）=x2-2x+1=（x-1）2≥0，
∴M≥N．
故选：D．
∴M-N=（3x2-5x+2）-（2x2-3x+1）=x2-2x+1=（x-1）2≥0，
∴M≥N．
故选：D．
点评：此题主要考查了公式法分解因式以及非负数的性质，得出M-N的值是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
下列命题中是假命题的是（ ）
| A、三角形的一条中线将三角形分成面积相等的两部分 |
| B、三角形的三条角平分线相交于一点 |
| C、三角形的三条高相交于一点 |
| D、三角形的任意两边之和大于第三边 |
5的相反数是（ ）
A、
| ||
B、-
| ||
| C、5 | ||
| D、-5 |
某同学随机将一枚硬币抛向空中20次，有12次出现反面，那么正面出现的频率是（ ）
| A、0.12 | B、0.4 |
| C、0.8 | D、0.6 |
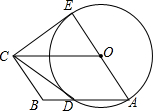如图，四边形OABC是平行四边形，以O为圆心，OA为半径的圆交AB于点D，延长AO交⊙O于点E，连接CD，CE，若CE是⊙O的切线，解答下列问题：