题目内容
18.已知等腰三角形一腰上的高与另一腰的夹角为50°,求这个等腰三角形的底角的度数.分析 分两种情况讨论:①若∠A<90°;②若∠A>90°;先求出顶角∠BAC,即可求出底角的度数.
解答 解:分两种情况讨论:
①若∠A<90°,如图1所示: ∵BD⊥AC,
∵BD⊥AC,
∴∠A+∠ABD=90°,
∵∠ABD=50°,
∴∠A=90°-50°=40°,
∵AB=AC,
∴∠ABC=∠C=$\frac{1}{2}$(180°-40°)=70°;
②若∠A>90°,如图2所示: 同①可得:∠DAB=90°-50°=40°,
同①可得:∠DAB=90°-50°=40°,
∴∠BAC=180°-40°=140°,
∵AB=AC,
∴∠ABC=∠C=$\frac{1}{2}$(180°-140°)=20°;
综上所述:等腰三角形底角的度数为70°或20°
点评 本题考查了等腰三角形的性质以及余角和邻补角的定义;注意分类讨论方法的运用,避免漏解.

练习册系列答案
相关题目
13.已知a+13=b+9=c+3,则a2+b2+c2-ab-cb-ac=( )
| A. | 259 | B. | 179.5 | C. | 76 | D. | 152 |
3.下列各式中,能用平方差公式分解因式的是( )
| A. | x2+y2 | B. | x2-2x+1 | C. | -x2+y2 | D. | -x2-y2 |
7.青山村种的水稻2010年平均每公顷产7200kg,2012年水稻平均每公顷产的产量是8400kg,设水稻每公顷产量的年平均增长率为x,可列方程为( )
| A. | 7200(1+x)2=8400 | B. | 7200(1+x2)=8400 | C. | 7200(x2+x)=8400 | D. | 7200(1+x)=8400 |
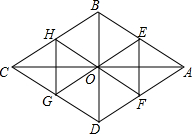 如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.
如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.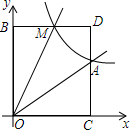 已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,2).
已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,2).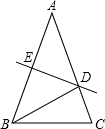 如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D.
如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D.