题目内容
17.(1)解方程:x2+4x-2=0(2)解不等式组:$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1}\\{1-3(x-1)<8-x}\end{array}\right.$.
分析 (1)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可;
(2)求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:(1)x2+4x-2=0,
x2+4x=2,
x2+4x+4=2+4,
(x+2)2=6,
x+2=$±\sqrt{6}$,
x1=-2+$\sqrt{6}$,x2=-2-$\sqrt{6}$;
(2)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1①}\\{1-3(x-1)<8-x②}\end{array}\right.$
∵解不等式①得:x≤1,
解不等式②得:x>-2,
∴不等式组的解集是-2<x≤1.
点评 本题考查了解一元一次不等式组,解一元二次方程的应用,能正确配方是解(1)的关键,能根据找不等式组解集的规律找出不等式组的解集是解(2)的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
7.青山村种的水稻2010年平均每公顷产7200kg,2012年水稻平均每公顷产的产量是8400kg,设水稻每公顷产量的年平均增长率为x,可列方程为( )
| A. | 7200(1+x)2=8400 | B. | 7200(1+x2)=8400 | C. | 7200(x2+x)=8400 | D. | 7200(1+x)=8400 |
12.若△ABC∽△DEF,且面积比为1:3,则△ABC与△DEF的周长比为( )
| A. | 1:3 | B. | 1:9 | C. | 1:$\sqrt{3}$ | D. | 3:1 |
9.下列说法:
①0是绝对值最小的有理数;
②相反数大于本身的数是负数;
③有理数分为正数和负数;
④有理数都可以用数轴上的点表示.
其中正确的是( )
①0是绝对值最小的有理数;
②相反数大于本身的数是负数;
③有理数分为正数和负数;
④有理数都可以用数轴上的点表示.
其中正确的是( )
| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
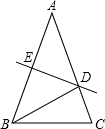 如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D.
如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D. 一个小立方块的六个面分别标有数字1,2,3,4,5,6,从三个不同方向看到的情形如图所示,则如图放置时三个底面上的数字之和等于(
一个小立方块的六个面分别标有数字1,2,3,4,5,6,从三个不同方向看到的情形如图所示,则如图放置时三个底面上的数字之和等于(