题目内容
8.在等边△ABC中,E是边BC上的一个动点(不与点B,C重合),∠AEF=60°,EF交△ABC外角平分线CD于点F.(1)如图1,当点E是BC的中点时,请你补全图形,直接写出$\frac{CF}{AE}$的值,并判断AE与EF的数量关系;
(2)当点E不是BC的中点时,请你在图(2)中补全图形,判断此时AE与EF的数量关系,并证明你的结论.
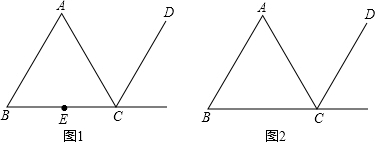
分析 (1)由等边三角形的性质得到∠EAC=30°,得到∠CEF=30°,求得∠ECF=120°,得到∠EFC=30°,推出AC垂直平分EF,得到△AEF是等边三角形,于是得到结论;
(2)连接AF,EF与AC交于点G.由CD是它的外角平分线.得到∠ACF=60°=∠AEF,根据相似三角形的性质得到$\frac{GE}{GA}=\frac{GC}{GF}$,∠AFE=∠ACB=60°,得到△AEF为等边三角形,于是得到结论.
解答  解:(1)$\frac{CF}{AE}=\frac{{\sqrt{3}}}{3}$;
解:(1)$\frac{CF}{AE}=\frac{{\sqrt{3}}}{3}$;
∵△ABC是等边三角形,点E是BC的中点,
∴∠EAC=30°,
∵∠AEF=60°,
∴∠CEF=30°,
∵CD平分△ABC外角,
∴∠ECF=120°,
∴∠EFC=30°,
∴CE=CF,
∴AC垂直平分EF,
∴AE=AF;
∴△AEF是等边三角形,
∴AE=EF;
(2)连接AF,EF与AC交于点G.
∵在等边△ABC中,CD是它的外角平分线.
∴∠ACF=60°=∠AEF,
∵∠AGE=∠FGC
∴△AGE∽△FGC,
∴$\frac{GE}{GC}=\frac{GA}{GF}$,
∴$\frac{GE}{GA}=\frac{GC}{GF}$,
∵∠AGF=∠EGC,
∴△AGF∽△EGC,
∵∠AFE=∠ACB=60°,
∴△AEF为等边三角形,
∴AE=EF.
点评 本题考查了相似三角形的判定和性质,等边三角形的判定和性质,角平分线的定义,正确的作出图形是解题的关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2016B2017C2017的顶点B2017的坐标是(21008,21008).
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2016B2017C2017的顶点B2017的坐标是(21008,21008). 如图,E为正方形ABCD对角线BD上一点,且BE=BC,则∠DCE=22.5°.
如图,E为正方形ABCD对角线BD上一点,且BE=BC,则∠DCE=22.5°.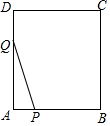 如图,长方形ABCD中,AB=10cm,AD=12cn,∠A=90°,点P从点A开始沿着AB边以5cm/s的速度移动,同时另一点Q由A点开始以12cm/s的速度沿着AD边移动.设两点的运动时间为t秒.
如图,长方形ABCD中,AB=10cm,AD=12cn,∠A=90°,点P从点A开始沿着AB边以5cm/s的速度移动,同时另一点Q由A点开始以12cm/s的速度沿着AD边移动.设两点的运动时间为t秒.
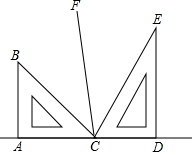 把两个三角尺按如图所示那样拼在一起(三角尺分别含30°,45°,60°,90°角,点A、C、D在一条直线上).
把两个三角尺按如图所示那样拼在一起(三角尺分别含30°,45°,60°,90°角,点A、C、D在一条直线上).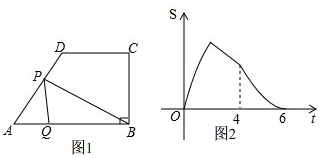 如图,已知四边形ABCD中,AB∥CD,∠ABC=90°,AB=2CD,点P从点A出发以每秒2个单位沿折线AD-DC-CB运动,同时点Q从点A出发以每秒1个单位向点B运动,当其中一个点到达终点时,另一个点也停止运动,连结PQ、PB,设△PBQ的面积为S,运动时间为t秒,S关于t的大致函数图象如图所示.
如图,已知四边形ABCD中,AB∥CD,∠ABC=90°,AB=2CD,点P从点A出发以每秒2个单位沿折线AD-DC-CB运动,同时点Q从点A出发以每秒1个单位向点B运动,当其中一个点到达终点时,另一个点也停止运动,连结PQ、PB,设△PBQ的面积为S,运动时间为t秒,S关于t的大致函数图象如图所示.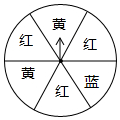 转动如图所示的转盘一次,当转盘停止转动时,记录指针所指向区域的颜色(若指针落在交界处,则重转一次)
转动如图所示的转盘一次,当转盘停止转动时,记录指针所指向区域的颜色(若指针落在交界处,则重转一次)