题目内容
18．有若干个数，第1个记为a1，第2个记为a2，第n个记为an．若a1=$-\frac{1}{2}$，从第2数起后面每一个数都等于1与它前面的那个数的差的倒数，则a3=3，a2012=$\frac{2}{3}$．分析 根据1与它前面那个数的差的倒数，即an+1=$\frac{1}{1-{a}_{n}}$，即可求得a2；然后根据得到结果出现的规律，即可确定a2012．
解答 解：a1=$-\frac{1}{2}$，
a2=$\frac{1}{1-（-\frac{1}{2}）}$=$\frac{2}{3}$，
a3=$\frac{1}{1-\frac{2}{3}}$=3，
a4=$\frac{1}{1-3}$=-$\frac{1}{2}$，
…
-$\frac{1}{2}$，$\frac{2}{3}$，3三个数依次不断循环，
2012÷3=670…2，则a2012=a2=$\frac{2}{3}$．
故答案为：3，$\frac{2}{3}$．
点评 此题考查数字的变化规律，找出数字之间的联系，得出运算规律，利用规律解决问题．
练习册系列答案
互动课堂系列答案
相关题目
如图，抛物线的顶点A（-3，-3），且经过原点O．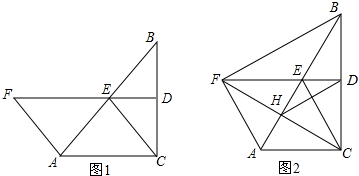
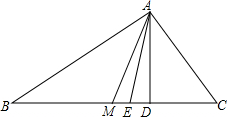已知：如图，在△ABC中，AB＞AC，AM是中线，AD是高，AE是角平分线，并且∠DAE=∠MAE，求证：∠BAC=90°．
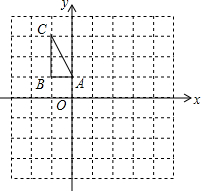如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（0，1），B（-1，1），C（-1，3）．
7．二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
下列结论中正确的有4个．
（1）ac＜0；
（2）当x＞1时，y的值随x值的增大而减小；
（3）x=2是方程ax2+（b-1）x+c=0的一个根；
（4）当-1＜x＜2时，ax2+（b-1）x+c＞0．
| x | -1 | 0 | 0.5 | 2 |
| y | -1 | 2 | 3.75 | 2 |
（1）ac＜0；
（2）当x＞1时，y的值随x值的增大而减小；
（3）x=2是方程ax2+（b-1）x+c=0的一个根；
（4）当-1＜x＜2时，ax2+（b-1）x+c＞0．