题目内容
某校八年级(1)班共有35名学生,其中
的男生和
的女生骑自行车上学,那么该班骑自行车上学的学生的人数最少是 人.
| 1 |
| 2 |
| 1 |
| 3 |
考点:二元一次方程的应用
专题:
分析:设有a个男生骑车,b个女生骑车,则可得2a+3b=35,求a+b的最小值即可得出答案.
解答:解:设有a个男生骑车,b个女生骑车,则题目可简写成2a+3b=35,
解法①:当b=1时,a=16;
当b=2时,b=
;
当b=3时,a=13;
当b=4时,a=
;
当b=5时,a=10;
当b=6时,a=
;
当b=7时,a=7;
当b=8时,a=
;
当b=9时,a=4;
当b=10时,a=
;
当b=11时,a=1;
∵a、b均为正整数,
∴可得a+b的最小值为12,即该班骑自行车上学的学生的人数最少12人.
解法②:∵2a+3b=35,
∴a=
,a+b=
,b≤11.
故可得当b=11时,a+b的值最小,最小值为12.
故答案为:12.
解法①:当b=1时,a=16;
当b=2时,b=
| 29 |
| 2 |
当b=3时,a=13;
当b=4时,a=
| 23 |
| 2 |
当b=5时,a=10;
当b=6时,a=
| 17 |
| 2 |
当b=7时,a=7;
当b=8时,a=
| 11 |
| 2 |
当b=9时,a=4;
当b=10时,a=
| 5 |
| 2 |
当b=11时,a=1;
∵a、b均为正整数,
∴可得a+b的最小值为12,即该班骑自行车上学的学生的人数最少12人.
解法②:∵2a+3b=35,
∴a=
| 35-3b |
| 2 |
| 35-b |
| 2 |
故可得当b=11时,a+b的值最小,最小值为12.
故答案为:12.
点评:此题考查了二元一次方程的应用,解答本题的关键是设出未知数,得出二元一次方程,根据a、b均为正整数进行解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一个数除以它的倒数,商为1,这个数是( )
| A、1 | B、2 | C、-1 | D、-1或+1 |
一元二次方程x2+x-3=0的根的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、只有一个实数根 |
| D、没有实数根 |
 如图,Rt△ABC中∠ACB=90°,DE垂直平分AC交AB于E,∠A=30°,DE=4,则BE=
如图,Rt△ABC中∠ACB=90°,DE垂直平分AC交AB于E,∠A=30°,DE=4,则BE=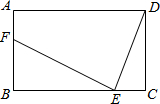 如图,在矩形ABCD中,AB=6,BC=9,E为线段BC上的动点(不与B、C重合).连接DE,作EF⊥DE,EF与线段AB交于点F,设CE=x.
如图,在矩形ABCD中,AB=6,BC=9,E为线段BC上的动点(不与B、C重合).连接DE,作EF⊥DE,EF与线段AB交于点F,设CE=x.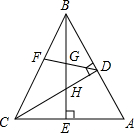 在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,F为BC中点,BE平分∠ABC,已证△BDH≌△CDA,求证:BG2-GE2=AE2.
在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,F为BC中点,BE平分∠ABC,已证△BDH≌△CDA,求证:BG2-GE2=AE2.