题目内容

已知三角形的三边分别为
16a2+b2
、
4a2+9b2
、2
a2+b2
，求这个三角形的面积．
考点：面积及等积变换
专题：
分析：利用矩形ABCD，构造△EFC符合边长：FC=
16a2+b2
、EC=
4a2+9b2
、EF=2
a2+b2
，利用S△EFC=S矩形ABCD-F△FBC-S△AEF-S△EDC求值即可．
解答：解：如图构造矩形ABCD，AB=3b，BC=4a，在AB上取点F使FB=b，在AD上取点E使AE=2a，则△EFC符合题中边长：FC=
16a2+b2
、EC=
4a2+9b2
、EF=2
a2+b2
，

所以S△EFC=S矩形ABCD-F△FBC-S△AEF-S△EDC=12ab-2ab-2ab-3ab=5ab．
点评：本题主要考查了面积及等积变换，解题的关键是构造边长为
16a2+b2
、
4a2+9b2
、2
a2+b2
的三角形．
练习册系列答案
相关题目
某同学把7×（□-3）错抄为7×□-3，抄错后算得答案为y，若正确答案为x，则x-y=
 
．
运用乘法公式计算（m-2n+3）（m+2n-3）=
 
．
如图，用火柴拼三角形，则第n个图需用火柴
 
根．
如图所示，若△ABE≌△ACF，且AB=5，AE=3，则EC的长为
 
．
在相同的时刻，太阳光下物高与影长成正比．如果高为1.5米的人的影长为2.5米，那么影长为30米的旗杆的高是（　　）
A、18米B、16米
C、20米D、15米
如图，在等腰梯形ABCD中，AD∥BC，AB=CD=AD=2cm，∠BAD=120°，P为AD的中点，在直线AD下方作∠BPE=120°，使边PE与等腰梯形的某一边所在直线相交于点E．
（1）画出所有符合题意的示意图，并说明以点B、P、E为顶点的三角形是否与△ABP相似？
（2）求△BPA的面积．
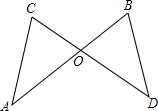如图，△OCA≌△OBD，AO=3，CO=2，则AB的长为（　　）
A、1B、3C、4D、5
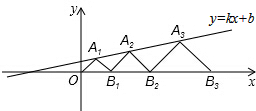在平面直角坐标系xOy中，点A1，A2，A3…和B1，B2，B3…分别在直线y=kx+b和x轴上，△OA1B1，△B1A2B2，△B2A3B3，…都是等腰直角三角形，如果A1（1，1），A2（
7
2
，
3
2
），那么点A3的纵坐标是
 
，点A2014的纵坐标是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网