题目内容
12.⊙O的弦AB所对的劣弧是圆的$\frac{1}{6}$,⊙O半径为4cm,则AB=4cm,弦AB所对的圆周角的度数为30°或150°.分析 首先根据题意画出图形,求得弦AB所对圆心角的度数,则△OAB是等边三角形,即可求得AB的长,根据圆周角定理即可求得弦AB所对的圆周角的度数.
解答 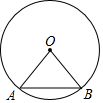 解:弦AB所对的圆心∠AOB=$\frac{1}{6}$×360°=60°,
解:弦AB所对的圆心∠AOB=$\frac{1}{6}$×360°=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴AB=OA=4(cm).
当弦AB所对的圆周角在优弧上时,度数是$\frac{1}{2}$×60°=30°;
当选AB所对的圆心角在劣弧上时,度数是$\frac{1}{2}$×(360°-60°)=150°.
故答案是:4cm; 30°或150°.
点评 此题考查了圆周角定理,此题难度适中,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
相关题目
2.如果a与-7互为倒数,那么a是( )
| A. | 0 | B. | -$\frac{1}{7}$ | C. | 7 | D. | 1 |
2.若3x-2nym与xmy-3n的积与$\frac{1}{2}$x4y3是同类项,则m+2n的立方根( )
| A. | -2 | B. | 2 | C. | ±2 | D. | 8 |
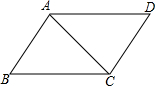 如图,已知AD∥BC,AD=BC.求证:△ADC≌△CBA.
如图,已知AD∥BC,AD=BC.求证:△ADC≌△CBA.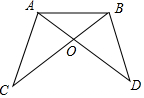 如图,在△ABC和△BAD中,因为AB=BA,∠ABC=∠BAD,BC=AD,根据“SAS”可以得到△ABC≌△BAD.
如图,在△ABC和△BAD中,因为AB=BA,∠ABC=∠BAD,BC=AD,根据“SAS”可以得到△ABC≌△BAD.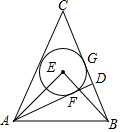 如图,在等腰△ABC中,CA=CB,AD是腰BC边上的高,△ACD的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE.
如图,在等腰△ABC中,CA=CB,AD是腰BC边上的高,△ACD的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE.